Betrag eines Vektors
Formeln und Beispiele zur Berechnung der Vektorlänge und des Betrags
Der Betrag eines Vektors (auch Magnitude, Länge oder Norm genannt) ist eine skalare Größe, die die Länge des Vektors im Raum angibt. Der Betrag wird mit Hilfe des Satzes des Pythagoras berechnet und ist eine fundamental wichtige Größe in der Vektorrechnung und Physik.
Der Betrag eines Vektors ist immer eine nicht-negative reelle Zahl und wird notiert als \(|\vec{v}|\), \(\|\vec{v}\|\) oder manchmal auch \(\text{mag}(\vec{v})\).
Grundkonzept: Der Satz des Pythagoras
Die Berechnung des Betrags basiert auf dem Satz des Pythagoras. Geometrisch kann ein Vektor als die Hypotenuse eines rechtwinkligen Dreiecks interpretiert werden, dessen Katheten den Komponenten des Vektors entsprechen.
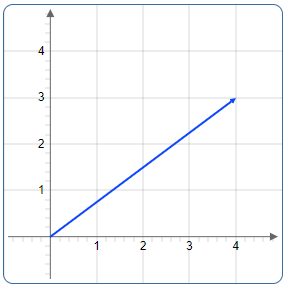
Der Vektor \(\begin{bmatrix} 4 \\ 3 \end{bmatrix}\) als Hypotenuse eines rechtwinkligen Dreiecks mit Katheten 4 und 3
Nach dem Satz des Pythagoras gilt:
Formeln für den Betrag
Betrag eines 2D-Vektors
Für einen Vektor \(\vec{v} = \begin{bmatrix} x \\ y \end{bmatrix}\):
Betrag eines 3D-Vektors
Für einen Vektor \(\vec{v} = \begin{bmatrix} x \\ y \\ z \end{bmatrix}\):
Allgemeine Formel für n-dimensionale Vektoren
Für einen Vektor \(\vec{v} = \begin{bmatrix} v_1 \\ v_2 \\ \vdots \\ v_n \end{bmatrix}\):
Betragsquadrat
Das Quadrat des Betrags (oft für Berechnungen praktischer):
Praktische Beispiele
Beispiel 1: 2D-Vektor
Gegeben: \(\vec{v} = \begin{bmatrix} 3 \\ 4 \end{bmatrix}\)
Beispiel 2: 3D-Vektor mit kleinen Zahlen
Gegeben: \(\vec{a} = \begin{bmatrix} 1 \\ 2 \\ 2 \end{bmatrix}\)
Beispiel 3: 3D-Vektor mit größeren Zahlen
Gegeben: \(\vec{b} = \begin{bmatrix} -4 \\ 6 \\ -12 \end{bmatrix}\)
Beispiel 4: Betragsquadrat
Gegeben: \(\vec{v} = \begin{bmatrix} 3 \\ 4 \end{bmatrix}\), Betragsquadrat berechnen:
Beispiel 5: Vektor mit negativen Komponenten
Gegeben: \(\vec{c} = \begin{bmatrix} -5 \\ -12 \end{bmatrix}\)
Das Vorzeichen der Komponenten spielt keine Rolle, da diese quadriert werden. Der Betrag ist daher immer nicht-negativ: \(|\vec{v}| \geq 0\)
Eigenschaften des Betrags
- \(|\vec{v}| \geq 0\) für alle Vektoren (nicht-negative Eigenschaft)
- \(|\vec{v}| = 0 \iff \vec{v} = \vec{0}\) (nur der Nullvektor hat Betrag 0)
- \(|k \cdot \vec{v}| = |k| \cdot |\vec{v}|\) für ein Skalar \(k\) (Skalierungseigenschaft)
- \(|\vec{v} + \vec{w}| \leq |\vec{v}| + |\vec{w}|\) (Dreiecksungleichung)
- \(|\vec{v} \cdot \vec{w}| \leq |\vec{v}| \cdot |\vec{w}|\) (Cauchy-Schwarz-Ungleichung)
Normalisierung: Einheitsvektor
Ein Einheitsvektor ist ein Vektor mit dem Betrag 1. Jeden Vektor kann man normalisieren, indem man ihn durch seinen Betrag teilt.
Formel der Normalisierung
Beispiel: Normalisierung eines 2D-Vektors
Gegeben: \(\vec{v} = \begin{bmatrix} 3 \\ 4 \end{bmatrix}\), wir wissen \(|\vec{v}| = 5\)
Verifikation des Betrags:
Zusammenfassung
2D-Betrag
\[\displaystyle |\vec{v}| = \sqrt{x^2 + y^2}\]
3D-Betrag
\[\displaystyle |\vec{v}| = \sqrt{x^2 + y^2 + z^2}\]
Allgemein
\[\displaystyle |\vec{v}| = \sqrt{\sum_{i=1}^{n} v_i^2}\]
Normalisierung
\[\displaystyle \hat{v} = \frac{\vec{v}}{|\vec{v}|}\]
|
|