RLC Parallelschaltung berechnen
Rechner und Formeln zur Berechnung von Spannung und Leistung einer RLC Parallelschaltung
RLC Parallelschaltung berechnen
RLC Parallelschaltung
Diese Funktion berechnet Leistungen, Strom, Schein- und Blindwiderstand einer Parallelschaltung aus Widerstand, Spule und Kondensator bei gegebener Frequenz.
RLC Parallelschaltung
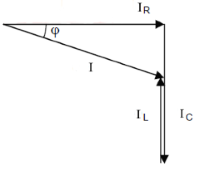
Parallelschaltung Eigenschaften
- Gleiche Spannung an allen Bauteilen
- Geometrische Addition der Teilströme
- IL und IC sind um 180° phasenverschoben
- Gesamtstrom kann kleiner als größter Teilstrom sein
Grundformeln
Strom- und Leitwertdreieck nach Pythagoras
Leitwerte (Admittanz)
- G: Wirkleitwert = 1/R
- BL: Induktiver Blindleitwert = 1/XL
- BC: Kapazitiver Blindleitwert = 1/XC
- Y: Scheinleitwert = 1/Z
|
|
|
|
RLC Parallelschaltung - Theorie und Formeln
Grundlagen der RLC Parallelschaltung
Der Gesamtwiderstand der RLC-Parallelschaltung im Wechselstromkreis wird als Scheinwiderstand oder Impedanz Z bezeichnet. Für die Gesamtschaltung gilt das Ohmsche Gesetz. Der Gesamtstrom I ist die Summe der geometrisch addierten Teilströme.
Stromdreieck
Ströme
Leitwertdreieck
Blindwiderstände und Ströme
Blindwiderstände
Frequenzabhängige Widerstände von Spule und Kondensator.
Teilströme
Alle Zweige haben die gleiche Spannung U.
Gesamtstrom
Geometrische Addition der Teilströme.
Leistungsdreieck
Leistungen
Phasenbeziehungen
Phasenlagen
- Widerstand R: Strom und Spannung in Phase
- Spule L: Spannung eilt Strom um +90° voraus
- Kondensator C: Spannung eilt Strom um -90° nach
- Resultierende Phase: Abhängig von IC - IL
Frequenzverhalten
Tiefe Frequenzen
- XC >> XL
- IC << IL
- Induktives Verhalten
- Positive Phasenverschiebung
Resonanzfrequenz
- IL = IC
- Z = R (maximal)
- φ = 0°
- Minimaler Gesamtstrom
Hohe Frequenzen
- XL >> XC
- IL << IC
- Kapazitives Verhalten
- Negative Phasenverschiebung
Praktische Anwendungen
Filter-Schaltungen:
Abstimmkreise:
Blindleistung:
Unterschiede zur Serienschaltung
Parallel vs. Serie
Parallelschaltung:
- Gleiche Spannung an allen Bauteilen
- Z maximal bei Resonanz
- I minimal bei Resonanz
- Stromaufteilung je nach Impedanz
Serienschaltung:
- Gleicher Strom durch alle Bauteile
- Z minimal bei Resonanz
- I maximal bei Resonanz
- Spannungsaufteilung je nach Impedanz
Design-Hinweise
Wichtige Designaspekte
- Stromaufteilung: Abhängig von Frequenz und Bauteilwerten
- Resonanz: Bei f₀ = 1/(2π√LC) ist Z maximal
- Stromüberhöhung: IL und IC können I deutlich überschreiten
- Verluste: ESR der Bauteile reduziert maximale Impedanz
- Belastung: Zusätzliche Last parallel reduziert Gesamtimpedanz
- Güte: Q = R/(XL oder XC) bei Resonanz
|
|