T-Dämpfungsglied

Rechner und Formeln zur Berechnung der Widerstände eines T-Dämpfungsglied

T-Dämpfungsglied Rechner

Eingabemodi

Geben Sie entweder die Dämpfung in dB oder das Spannungsverhältnis U₁/U₂ ein. Die Impedanz muss für beide Modi angegeben werden.

Eingabemodus wählen
Ω
dB
V
V
Ergebnisse
Serienwiderstand R₁:
Parallelwiderstand R₂:

T-Dämpfungsglied

T-Dämpfungsglied

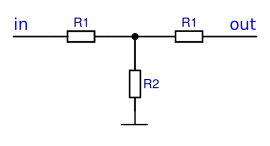
Schaltbild eines T-Dämpfungsglieds

Zweck und Anwendung
  • Impedanzanpassung bei hohen Frequenzen
  • Eingangs- und Ausgangsimpedanz gleich der Wellenimpedanz
  • Kontrollierte Signaldämpfung ohne Verzerrung
  • T-förmige Widerstandsanordnung
Eingabemodi
Dämpfung in dB: Direkte Eingabe des Dämpfungsmaßes
Spannungsverhältnis: Verhältnis U₁/U₂ der Ein- und Ausgangsspannung
Wichtiger Hinweis
Bei Dämpfungsgliedern für hohe Frequenzen muss auf die Impedanzanpassung geachtet werden. Die Eingangs- und Ausgangsimpedanz müssen gleich der Wellenimpedanz der Leitungen sein.

Formeln zum T-Dämpfungsglied

Grundlegende Formeln

Die Widerstände R₁ und R₂ des T-Dämpfungsglieds errechnen sich aus der Impedanz Z und dem Dämpfungsfaktor a. Der Dämpfungsfaktor a berechnet sich aus dem Verhältnis der Ausgangsspannung zur Eingangsspannung (U₁ / U₂), bzw. dem Dämpfungsmaß ΔL in dB.

Dämpfungsfaktor
\[a = \frac{U_1}{U_2} = 10^{\frac{\Delta L}{20 \text{ dB}}}\]

Verhältnis von Ein- zu Ausgangsspannung

Serienwiderstand R₁
\[R_1 = Z \frac{a-1}{a+1}\]

Widerstände in der Signalleitung

Parallelwiderstand R₂
\[R_2 = Z \frac{2a}{a^2-1}\]

Widerstand zwischen den Leitungen

Praktische Rechenbeispiele

Beispiel 1: 6dB Dämpfung bei 50Ω

Gegeben: Z = 50Ω, ΔL = 6dB

1. Dämpfungsfaktor: \[a = 10^{\frac{6}{20}} = 10^{0,3} = 1{,}995\]
2. R₁: \[R_1 = 50 \times \frac{1{,}995-1}{1{,}995+1} = 50 \times \frac{0{,}995}{2{,}995} = 16{,}6Ω\]
3. R₂: \[R_2 = 50 \times \frac{2 \times 1{,}995}{1{,}995^2-1} = 50 \times \frac{3{,}99}{2{,}98} = 66{,}9Ω\]

Standard 6dB-Dämpfung für 50Ω-Systeme

Beispiel 2: 10dB Dämpfung bei 75Ω

Gegeben: Z = 75Ω, ΔL = 10dB

1. Dämpfungsfaktor: \[a = 10^{\frac{10}{20}} = 10^{0,5} = 3{,}162\]
2. R₁: \[R_1 = 75 \times \frac{3{,}162-1}{3{,}162+1} = 75 \times \frac{2{,}162}{4{,}162} = 39{,}0Ω\]
3. R₂: \[R_2 = 75 \times \frac{2 \times 3{,}162}{3{,}162^2-1} = 75 \times \frac{6{,}324}{8{,}998} = 52{,}7Ω\]

Typische Dämpfung für Kabel-TV-Anwendungen

Beispiel 3: Spannungsverhältnis bei 600Ω

Gegeben: Z = 600Ω, U₁ = 10V, U₂ = 2V

1. Dämpfungsfaktor: \[a = \frac{U_1}{U_2} = \frac{10V}{2V} = 5\]
2. Dämpfung in dB: \[\Delta L = 20 \times \log_{10}(5) = 20 \times 0{,}699 = 13{,}98dB\]
3. R₁: \[R_1 = 600 \times \frac{5-1}{5+1} = 600 \times \frac{4}{6} = 400Ω\]
4. R₂: \[R_2 = 600 \times \frac{2 \times 5}{5^2-1} = 600 \times \frac{10}{24} = 250Ω\]

Klassische Audiotechnik mit 600Ω-Impedanz

Anwendungen und Vergleich mit Pi-Dämpfungsglied

Typische Anwendungen

  • HF-Messtechnik: Kalibrierte Dämpfung für Messungen
  • Antennentechnik: Anpassung zwischen Sendern und Antennen
  • Kabel-TV: Signalpegeldämpfung in Verteilsystemen
  • Labormesstechnik: Definierte Signalabschwächung
  • EMV-Prüfungen: Kontrollierte Signalreduktion
  • Audiomesstechnik: Präzise Pegeldämpfung
Vergleich: T- vs. Pi-Dämpfungsglied
Eigenschaft T-Dämpfungsglied Pi-Dämpfungsglied
Aufbau 2×R₁ in Serie, R₂ parallel R₁ in Serie, 2×R₂ parallel
Impedanz-Verhalten Niederohmiger bei hoher Dämpfung Hochohmiger bei hoher Dämpfung
Anwendung Niederohmige Systeme bevorzugt Hochohmige Systeme bevorzugt
Symmetrie Symmetrisch aufgebaut Symmetrisch aufgebaut
Vorteile des T-Dämpfungsglieds
  • Konstante Impedanzanpassung
  • Gute Breitbandeigenschaften
  • Symmetrische Ein- und Ausgangsimpedanz
  • Niederohmiger Parallelwiderstand bei hoher Dämpfung
  • Geringere Verlustleistung im Parallelwiderstand
Design-Hinweise
  • Verwenden Sie Präzisionswiderstände (1% oder besser)
  • Achten Sie auf die Leistungsbelastbarkeit
  • Minimieren Sie parasitäre Kapazitäten bei HF
  • Verwenden Sie kurze, symmetrische Verbindungen
  • Berücksichtigen Sie Temperaturkoeffizienten
Praktische Tipps
  • Standard-Impedanzen: 50Ω (HF), 75Ω (Video), 600Ω (Audio)
  • Dämpfungswerte: 3dB, 6dB, 10dB, 20dB sind üblich
  • Für hohe Dämpfung: Kaskadierung mehrerer Stufen
  • Bei sehr hohen Frequenzen: Stripline-Technik verwenden
  • T-Glied bei niederohmigen Systemen bevorzugen
Weiterführende Rechner

Für alternative Topologie:

Pi-Dämpfungsglied

Frequenzverhalten und Anwendungsgrenzen

Frequenzabhängigkeit

Das T-Dämpfungsglied zeigt bei korrekter Dimensionierung ein gutes Breitbandverhalten. Die Grenzfrequenz wird hauptsächlich durch parasitäre Reaktanzen und die Bauteilgeometrie bestimmt.

DC bis 100MHz:
Diskrete Widerstände
Standardbauformen
100MHz bis 1GHz:
SMD-Bauformen
Kurze Verbindungen
Über 1GHz:
Stripline-Technik
Mikrowellendesign

Wahl zwischen T- und Pi-Glied: T-Dämpfungsglieder eignen sich besonders für niederohmige Systeme, da der Parallelwiderstand R₂ auch bei hoher Dämpfung noch relativ niederohmig bleibt.

Ist diese Seite hilfreich?            
Vielen Dank für Ihr Feedback!

Das tut uns leid

Wie können wir die Seite verbessern?


Weitere Rechner für Widerstände

Ohmsche Gesetz  •  Gesamtwiderstand 2 Parallelwiderstände  •  Gesamtwiderstand Parallelwiderstände  •  Spannungsteiler, unbelastet  •  Spannungsteiler, belastet  •  Vorwiderstand (Voltmeter)  •  Parallelwiderstand (Ampermeter)  •  Pi Dämpfungsglied  •  T Dämpfungsglied  •