Parallelwiderstand eines Ampermeters

Rechner und Formeln zur Berechnung des Parallelwiderstands zur Messbereichserweiterung

Parallelwiderstand Rechner

Messbereichserweiterung

Berechnung des Parallelwiderstands (Shunt) zur Erweiterung des Messbereichs eines Ampermeters. Wählen Sie zwischen Messwerkwiderstand oder Gesamtspannung als Eingabeparameter.

Eingabeparameter wählen

Messwerkwiderstand R_m eingeben

Gesamtspannung U_tot eingeben

Gesamtstrom I_tot

Messwerkstrom I_m

Messwerkwiderstand R_m

Gesamtspannung U_tot

Dezimalstellen

Ergebnisse

Parallelwiderstand R_p:

Leistung P_p:

Ampermeter Parallelwiderstand

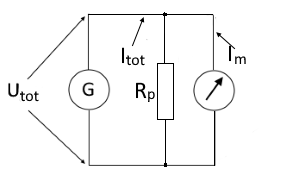
Schaltbild: Ampermeter mit Parallelwiderstand (Shunt)

Zweck des Parallelwiderstands

Messbereichserweiterung bei Ampermetern
Stromaufteilung zur Schonung des Messwerks
Ermöglicht Messung größerer Ströme
Verhindert Überlastung des Messgeräts

Eingabemodi

Messwerkwiderstand: Direkter Widerstandswert des Messwerks

Gesamtspannung: Spannungsabfall am gesamten Messkreis

Wichtiger Hinweis

Ein ideales Ampermeter sollte einen sehr niedrigen Innenwiderstand haben, um den zu messenden Stromkreis möglichst wenig zu beeinflussen.

Formeln zur Parallelwiderstand-Berechnung

Hauptformel über Messwerkwiderstand

Mit dem Verhältnis n = I_tot / I_m:

\[R_p = \frac{R_m}{n-1}\]

\[n = \frac{I_{tot}}{I_m}\]

Stromverhältnis bestimmt Parallelwiderstand

Gesamtwiderstand

Parallelschaltung von Messwerk und Shunt:

\[\frac{1}{R_{tot}} = \frac{1}{R_m} + \frac{1}{R_p}\]

Leitwerte werden addiert

Leistungsberechnung

Die Verlustleistung im Parallelwiderstand muss bei der Dimensionierung berücksichtigt werden:

\[P_p = I_p^2 \times R_p\]

\[I_p = I_{tot} - I_m\]

Praktisches Berechnungsbeispiel

Beispiel: Messbereichserweiterung von 2A auf 20A

Gegeben: Messwerk mit R_m = 10Ω, Messbereich 2A soll auf 20A erweitert werden

Schritt 1: Stromverhältnis berechnen

\[n = \frac{I_{tot}}{I_m} = \frac{20A}{2A} = 10\]

Schritt 2: Parallelwiderstand berechnen

\[R_p = \frac{R_m}{n-1} = \frac{10Ω}{10-1} = \frac{10Ω}{9} = 1{,}111Ω\]

Schritt 3: Stromverteilung prüfen

Durch das Messwerk: I_m = 2A
Durch den Shunt: I_p = 20A - 2A = 18A

Schritt 4: Leistung des Shunts

\[P_p = I_p^2 \times R_p = (18A)^2 \times 1{,}111Ω = 360W\]

Ergebnis: Parallelwiderstand R_p = 1,111Ω bei einer Verlustleistung von 360W

Theorie und praktische Anwendungen

Funktionsprinzip

Bei einem Ampermeter werden Parallelwiderstände (Shunts) verwendet, um den Messbereich zu erweitern. Der Parallelwiderstand wird parallel zum Messgerät geschaltet, um den Strom aufzuteilen. Dadurch fließt nur ein kleiner Teil des Gesamtstroms durch das empfindliche Messwerk.

Wichtige Eigenschaften

Stromaufteilung: Strom teilt sich umgekehrt proportional zu den Widerständen
Gleiche Spannung: Messwerk und Shunt haben dieselbe Spannung
Präzision: Shunt-Widerstände müssen sehr genau sein
Stabilität: Temperaturstabile Materialien verwenden

Praktische Anwendungen

Digitalmultimeter: Strommessung in verschiedenen Bereichen
Industrielle Messtechnik: Hochstrom-Überwachung
Energiemessung: Stromwandler in Energiezählern
Batteriemanagement: Ladestrom-Überwachung

Symbolverzeichnis

U_tot	Gesamtspannung = Messwerkspannung
I_tot	Gesamtstrom
I_m	Strom im Messwerk
R_m	Widerstand des Messwerks
R_p	Wert des Parallelwiderstands (Shunt)
P_p	Leistung/Belastbarkeit des Parallelwiderstands

Wichtige Hinweise

Shunt-Widerstand muss präzise dimensioniert sein
Leistungsbelastbarkeit des Shunts beachten
Temperaturkoeffizient berücksichtigen
Kontaktwiderstände minimieren
Kalibrierung nach Installation

Praktische Tipps

Manganin oder Konstantan als Shunt-Material
Kelvin-Anschluss für präzise Messung
Wärmeableitung bei hohen Strömen
Schutz vor mechanischen Belastungen
Regelmäßige Kalibrierung

Weitere Rechner für Widerstände

Ohmsche Gesetz • Gesamtwiderstand 2 Parallelwiderstände • Gesamtwiderstand Parallelwiderstände • Spannungsteiler, unbelastet • Spannungsteiler, belastet • Vorwiderstand (Voltmeter) • Parallelwiderstand (Ampermeter) • Pi Dämpfungsglied • T Dämpfungsglied •