Belasteten Spannungsteiler berechnen

Onlinerechner zur Berechnung der Werte an einem belasteten Spannungsteiler

Belasteter Spannungsteiler

Belastungseffekt

Ein Lastwiderstand RL parallel zu R₂ verändert das Teilungsverhältnis. Geben Sie entweder die gewünschte Ausgangsspannung U₂ oder den Lastwiderstand RL ein.

Lastparameter wählen
Ergebnisse
Spannungen
Spannung U₁:
Spannung U₂:
Widerstände
Lastwiderstand RL:
R₂ || RL:
Gesamtwiderstand:
Ströme
Strom durch R₁:
Strom durch R₂:
Strom durch RL:

Belasteter Spannungsteiler

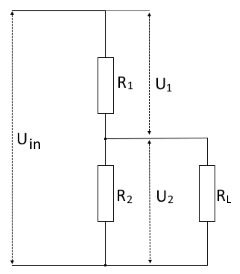
Schaltplan eines belasteten Spannungsteilers

Schaltbild: Belasteter Spannungsteiler mit Lastwiderstand RL

Belastungseffekt

Der Lastwiderstand RL parallel zu R₂ verändert:

  • Das Spannungsteilungsverhältnis
  • Die Ausgangsspannung U₂ (wird kleiner)
  • Den Gesamtstrom (wird größer)
  • Die Stromverteilung in der Schaltung
Hauptformel
\[U_2 = U_{in} \cdot \frac{R_{2L}}{R_1 + R_{2L}}\]
\[R_{2L} = \frac{R_2 \cdot R_L}{R_2 + R_L}\]
R2L = Parallelwiderstand von R₂ und RL
Wichtiger Hinweis
Je kleiner der Lastwiderstand RL, desto stärker wird die Ausgangsspannung U₂ reduziert. Für stabile Ausgangsspannungen sollte RL >> R₂ sein.


Formeln zum belasteten Spannungsteiler

1. Parallelwiderstand berechnen

Ersatzwiderstand von R₂ und RL:

\[R_{2L} = \frac{R_2 \cdot R_L}{R_2 + R_L}\]

Produktformel für Parallelschaltung

2. Ausgangsspannung

Modifizierte Spannungsteilerformel:

\[U_2 = U_{in} \cdot \frac{R_{2L}}{R_1 + R_{2L}}\]

Mit Parallelwiderstand R2L

3. Ströme berechnen

Nach dem Ohmschen Gesetz:

\[I_1 = \frac{U_1}{R_1}\]
\[I_2 = \frac{U_2}{R_2}, I_L = \frac{U_2}{R_L}\]
Zusätzliche Formeln

Lastwiderstand aus R2L berechnen:

\[R_L = \frac{R_2 \cdot R_{2L}}{R_2 - R_{2L}}\]

R2L aus Spannungen berechnen:

\[R_{2L} = \frac{U_2 \cdot R_1}{U_{in} - U_2}\]

Praktisches Berechnungsbeispiel

Beispiel: Belastungseffekt eines Spannungsteilers

Gegeben: Uin = 15V, R₁ = 10kΩ, R₂ = 20kΩ, RL = 30kΩ

Schritt 1: Unbelasteter Spannungsteiler (Referenz)
\[U_{2,unbelastet} = 15V \cdot \frac{20kΩ}{10kΩ + 20kΩ} = 15V \cdot \frac{20}{30} = 10V\]
Schritt 2: Parallelwiderstand R₂ || RL berechnen
\[R_{2L} = \frac{20kΩ \cdot 30kΩ}{20kΩ + 30kΩ} = \frac{600k}{50k} = 12kΩ\]
Schritt 3: Belastete Ausgangsspannung berechnen
\[U_{2,belastet} = 15V \cdot \frac{12kΩ}{10kΩ + 12kΩ} = 15V \cdot \frac{12}{22} ≈ 8{,}18V\]
Schritt 4: Ströme berechnen
Gesamtstrom: \[I_1 = \frac{15V}{22kΩ} ≈ 0{,}68mA\]
Strom durch R₂: \[I_2 = \frac{8{,}18V}{20kΩ} ≈ 0{,}41mA\]
Strom durch RL: \[I_L = \frac{8{,}18V}{30kΩ} ≈ 0{,}27mA\]
Schritt 5: Belastungseffekt bewerten
Spannungsabfall: 10V - 8,18V = 1,82V (18% Reduktion)
Stromerhöhung: 0,68mA vs. 0,5mA unbelastet (36% Erhöhung)
Fazit: Der Lastwiderstand von 30kΩ reduziert die Ausgangsspannung von 10V auf 8,18V. Für eine stabile Spannung sollte RL deutlich größer als R₂ gewählt werden.

Anwendungen und Designrichtlinien

Typische Anwendungen

  • Signalquellen: Spannungsteiler mit wechselnden Lasten
  • Sensor-Interfaces: Anpassung an verschiedene Eingangswiderstände
  • ADC-Vorverstärker: Berücksichtigung der Eingangsimpedanz
  • Audio-Schaltungen: Lautstärkeregler mit Kopfhörerlasten
  • Messschaltungen: Spannungsteiler mit Messgerätewiderständen
Designrichtlinien
  • Lastfaktor: RL sollte mindestens 10× größer als R₂ sein
  • Spannungsregulation: Für ±5% Genauigkeit: RL ≥ 20 × R₂
  • Stromverbrauch: Spannungsteiler-Strom >> Laststrom
  • Pufferung: Operationsverstärker für hochohmige Lasten verwenden
Vergleich mit unbelastetem Spannungsteiler
Parameter Unbelastet Belastet
Ausgangsspannung Konstant (ideal) Reduziert durch Last
Gesamtstrom Uin/(R₁+R₂) Höher durch Parallelwiderstand
Anwendung Referenzspannungen Signalquellen mit Last
Stabilität Sehr gut Abhängig von RL
Wichtige Hinweise
  • Lasteffekt: Jede angeschlossene Last verändert die Ausgangsspannung
  • Stromverbrauch: Höherer Stromverbrauch durch parallele Last
  • Temperaturgang: Alle Widerstände beeinflussen die Stabilität
  • Frequenzgang: Kapazitive Lasten können Instabilität verursachen
Weiterführende Rechner

Für unbelastete Anwendungen:

Unbelasteter Spannungsteiler
Praktische Tipps
  • Verwenden Sie Pufferverstärker für variable Lasten
  • Berechnen Sie worst-case Szenarien
  • Berücksichtigen Sie Toleranzen aller Widerstände
  • Überwachen Sie die Verlustleistung

Symboldefinitionen

UinEingangsspannung des Spannungsteilers
U₁Spannung an R₁
U₂Ausgangsspannung an R₂ || RL
R₁, R₂Spannungsteiler-Widerstände
RLLastwiderstand parallel zu R₂
R2LParallelwiderstand von R₂ und RL
I₁, I₂, ILStröme durch die jeweiligen Widerstände





Weitere Rechner für Widerstände

Ohmsche Gesetz  •  Gesamtwiderstand 2 Parallelwiderstände  •  Gesamtwiderstand Parallelwiderstände  •  Spannungsteiler, unbelastet  •  Spannungsteiler, belastet  •  Vorwiderstand (Voltmeter)  •  Parallelwiderstand (Ampermeter)  •  Pi Dämpfungsglied  •  T Dämpfungsglied  •