Flächeninhalt eines Dreiecks berechnen
Berechnung der Fläche eines Dreiecks aus zwei Seiten und einem Winkel
Dreiecksfläche Rechner
Flächenberechnung mit Sinus
Die Dreiecksfläche wird aus zwei Seiten und dem eingeschlossenen Winkel berechnet.
Visualisierung
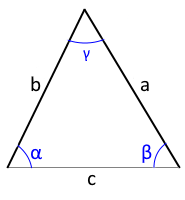
Das Diagramm zeigt ein Dreieck mit zwei Seiten und dem eingeschlossenen Winkel.
Die Fläche wird mit der Sinus-Formel berechnet.
Zuordnung der Winkel:
Zu den Seiten a, b wird der Winkel γ eingegeben.
Zu den Seiten b, c wird der Winkel α eingeben.
Zu den Seiten a, c wird der Winkel β eingeben.
|
|
Was ist die Dreiecksfläche?
Die Dreiecksfläche ist der Flächeninhalt des von drei Seiten umschlossenen Bereichs:
- Grundformel: A = ½ × Grundseite × Höhe
- Sinus-Formel: A = ½ × a × b × sin(γ)
- Eingeschlossener Winkel: Der Winkel zwischen den beiden gegebenen Seiten
- Einheit: Quadrateinheiten (m², cm², etc.)
- Anwendung: Bauplanung, Geometrie, Vermessung
- Vorteil: Einfache Berechnung aus zwei Seiten und Winkel
Die Sinus-Formel für Dreiecksflächen
Die Sinus-Formel ermöglicht die Flächenberechnung aus zwei Seiten und dem eingeschlossenen Winkel:
Mathematischer Hintergrund
- Basiert auf der trigonometrischen Sinus-Funktion
- Nutzt den Zusammenhang zwischen Winkel und Höhe
- Höhe h = b × sin(γ) bei Grundseite a
- Daraus folgt: A = ½ × a × b × sin(γ)
Praktische Vorteile
- Keine Höhenmessung erforderlich
- Direkte Berechnung aus verfügbaren Daten
- Funktioniert für alle Dreieckstypen
- Besonders nützlich in der Vermessung
Verschiedene Berechnungsmethoden
Es gibt verschiedene Formeln zur Flächenberechnung, je nach gegebenen Parametern:
Grundseite × Höhe
Klassische Formel bei bekannter Höhe
Sinus-Formel
Für zwei Seiten und eingeschlossenen Winkel
Heron-Formel
Für drei bekannte Seiten
Formeln zur Dreiecks-Flächenberechnung
Sinus-Formeln für verschiedene Seitenkombinationen
Seiten a, b mit Winkel γ
Seiten a, c mit Winkel β
Seiten b, c mit Winkel α
Grundformel
Grundseite mal Höhe geteilt durch 2
Vektoren-Formel
Kreuzprodukt zweier Vektoren
Heron-Formel
s = (a+b+c)/2 (Halbumfang)
Koordinaten-Formel
Für Dreiecke im Koordinatensystem
Symbole und Bezeichnungen
- A: Flächeninhalt des Dreiecks
- a, b, c: Seitenlängen des Dreiecks
- α, β, γ: Innenwinkel des Dreiecks
- h: Höhe des Dreiecks
- g: Grundseite (Basis) des Dreiecks
- s: Halbumfang (a+b+c)/2
- sin: Sinus-Funktion
- °: Grad (Winkelmaß)
Rechenbeispiel
Gegeben
Sinus-Formel anwenden
Einsetzen der gegebenen Werte
Berechnung
Die Fläche beträgt etwa 8,66 Flächeneinheiten
Kontrolle
- Plausibilität: Fläche ist positiv
- Größenordnung: Passt zu den Seitenlängen
- Spezialfall: Bei 90° wäre A = 10
Anwendungen
Landvermessung, Bauplanung, CAD-Software, Materialberechnung.
Dreiecksflächenberechnung in Theorie und Praxis
Die Flächenberechnung von Dreiecken ist eines der fundamentalsten Probleme der Geometrie und hat weitreichende Anwendungen in Mathematik, Physik, Ingenieurswesen und vielen anderen Bereichen. Die Sinus-Formel ist dabei besonders elegant und praktisch.
Die Sinus-Formel: Mathematischer Hintergrund
Die Sinus-Formel A = ½ab sin(γ) basiert auf der fundamentalen Beziehung zwischen Winkeln und Seitenverhältnissen in Dreiecken:
- Trigonometrische Grundlage: Die Höhe h auf die Seite a beträgt h = b × sin(γ)
- Flächenformel: A = ½ × Grundseite × Höhe = ½ × a × h = ½ × a × b × sin(γ)
- Universalität: Die Formel funktioniert für alle Dreieckstypen
- Symmetrie: Analoge Formeln existieren für alle drei Seitenkombinationen
Verschiedene Berechnungsmethoden
Klassische Methoden
- Grundseite × Höhe: A = ½gh (bei bekannter Höhe)
- Heron-Formel: A = √[s(s-a)(s-b)(s-c)] (drei Seiten)
- Sinus-Formel: A = ½ab sin(γ) (zwei Seiten, ein Winkel)
Moderne Ansätze
- Koordinaten-Geometrie: Determinanten-Formel
- Vektor-Algebra: Kreuzprodukt |a⃗ × b⃗|/2
- Komplexe Zahlen: Imaginärteil-Formel
Praktische Anwendungen
Die Dreiecksflächenberechnung findet sich in unzähligen praktischen Bereichen:
- Vermessungswesen: Grundstücksflächen, Triangulation, GPS-Berechnungen
- Bauwesen: Dachflächen, Konstruktionselemente, Materialberechnung
- Computergrafik: 3D-Rendering, Polygon-Meshes, Flächenberechnung
- Physik: Kräftediagramme, Schwerpunktberechnungen, Momentenanalyse
- Navigation: Peilung, Kursberechnungen, Standortbestimmung
- Landwirtschaft: Feldgrößen, Bewässerungsplanung, Ertragsschätzung
Vorteile der Sinus-Formel
Praktische Vorteile
- Keine Höhenmessung erforderlich
- Direkt aus verfügbaren Daten berechenbar
- Funktioniert für alle Dreieckstypen
- Besonders präzise bei bekannten Seitenlängen
Mathematische Eleganz
- Kompakte, symmetrische Formel
- Direkte trigonometrische Beziehung
- Erweiterbar auf beliebige Polygone
- Basis für weiterführende Berechnungen
Trigonometrische Grundlagen
Das Verständnis der Sinus-Funktion ist essentiell für die Flächenberechnung:
- Definition: sin(α) = Gegenkathete / Hypotenuse im rechtwinkligen Dreieck
- Wertebereich: -1 ≤ sin(α) ≤ 1 für alle Winkel α
- Spezialwerte: sin(30°) = 0.5, sin(60°) = √3/2, sin(90°) = 1
- Symmetrien: sin(180° - α) = sin(α), sin(α + 360°) = sin(α)
Fehlerquellen und Genauigkeit
Bei der praktischen Anwendung der Sinus-Formel sind verschiedene Aspekte zu beachten:
- Winkelmaß: Unterscheidung zwischen Grad und Radiant beachten
- Rundungsfehler: Ausreichende Dezimalstellen verwenden
- Messfehler: Ungenauigkeiten in Seitenlängen und Winkeln berücksichtigen
- Grenzfälle: Sehr spitze oder stumpfe Winkel können Probleme verursachen
Historische Entwicklung
Die Dreiecksflächenberechnung hat eine lange mathematische Geschichte:
- Antike: Bereits den Babyloniern und Ägyptern bekannt
- Griechenland: Euklid systematisierte die Flächenlehre
- Mittelalter: Arabische Mathematiker entwickelten die Trigonometrie
- Renaissance: Präzise trigonometrische Tafeln ermöglichten genaue Berechnungen
- Moderne: Computeralgorithmen für hochpräzise Berechnungen
Erweiterungen und Verallgemeinerungen
Die Grundprinzipien lassen sich auf komplexere Geometrien erweitern:
- Vielecke: Zerlegung in Dreiecke für Flächenberechnung
- 3D-Geometrie: Oberflächenberechnungen von Polyedern
- Sphärische Trigonometrie: Dreiecke auf Kugeloberflächen
- Analytische Geometrie: Integration für krummlinig begrenzte Flächen
Zusammenfassung
Die Sinus-Formel für Dreiecksflächenberechnung ist ein elegantes mathematisches Werkzeug mit breiten praktischen Anwendungen. Sie verbindet grundlegende trigonometrische Konzepte mit geometrischen Fragestellungen und bildet die Basis für viele weiterführende Berechnungen in Wissenschaft und Technik. Ihre Einfachheit und Universalität machen sie zu einem unverzichtbaren Bestandteil der mathematischen Grundausbildung.
|
|
|
|