Calculate Slope of a Line
Online calculator for calculating the slope between two points
Slope Calculator
Slope of a Line
The slope m of a line describes by how many units the Y-value changes when the X-value increases by one unit.
Visualization
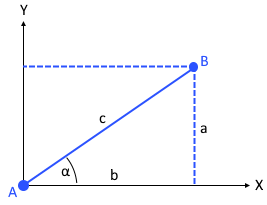
The graphic shows the slope as the ratio of height difference to horizontal distance.
The slope triangle illustrates the geometric meaning of the slope.
|
|
What is the Slope of a Line?
The slope indicates how steeply a line rises or falls:
- Positive slope: Line rises from left to right
- Negative slope: Line falls from left to right
- Slope = 0: Horizontal line (parallel to X-axis)
- Slope = 1: 45° rise (m = tan(45°))
- Large slope: Steep line
- Small slope: Flat line
Relationship Between Slope and Angle
The slope and the inclination angle are in direct relationship to each other:
Slope from Angle
Slope is the tangent of the angle
Angle from Slope
Angle is the arctangent of the slope
Formulas for Slope Calculation
Main Formula - Slope Between Two Points
Slope = Change in Y-direction ÷ Change in X-direction
Angle to X-axis (Arcsine)
Calculation via the sine of the slope triangle
Angle to X-axis (Arccosine)
Calculation via the cosine of the slope triangle
Distance Between Points
Hypotenuse of the slope triangle
Slope via Tangent
Direct relationship between slope and angle
Example
Example Calculation
Calculate Slope
The slope is 4/3 ≈ 1.33
Calculate Angle
The inclination angle is approximately 53.13°
Interpretation
- Slope 4/3: Y rises by 4 for every 3 X-units
- Positive slope: Line rises
- Steep rise: Angle > 45°
Applications
Road gradients, roof slopes, terrain profiles, technical drawings.
Understanding Slope in Practice
The slope of a line is a fundamental concept in mathematics and describes how steeply a line rises or falls. It is defined as the ratio of the vertical change to the horizontal change between two points.
Geometric Meaning
The slope m of a line between two points A(x₁,y₁) and B(x₂,y₂) is calculated as:
Types of Slope
Positive Slope (m > 0)
The line rises from left to right. The larger the value, the steeper the rise.
Negative Slope (m < 0)
The line falls from left to right. The more negative the value, the steeper the fall.
Zero Slope (m = 0)
The line runs horizontally. There is no change in Y-direction.
Infinite Slope
For vertical lines, the slope is undefined (division by zero).
Practical Applications
Slope calculation is found in many practical areas:
- Construction: Roof slopes, ramps, road gradients
- Geography: Terrain profiles, contour lines on maps
- Economics: Growth rates, trends in charts
- Physics: Velocity-time diagrams, force-displacement diagrams
- Engineering: Mechanical engineering, electronics (characteristic curves)
Special Slope Values
m = 1
45° rise
α = arctan(1) = 45°
m = √3 ≈ 1.73
60° rise
α = arctan(√3) = 60°
m = 1/√3 ≈ 0.58
30° rise
α = arctan(1/√3) = 30°
|
|
|
|