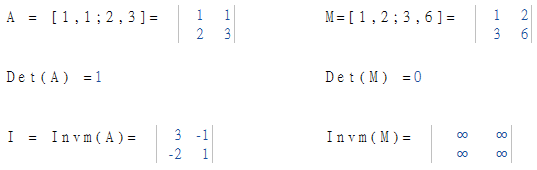Invertiert eine Matrix
Die Funktion \(Invm\) invertiert eine quadratische, nicht singuläre Matrix.
Sie können nur eine Inverse finden, wenn es sich um eine quadratische und nicht singuläre Matrix handelt. Ob es sich um eine nicht singuläre Matrix handelt, können Sie durch die Berechnung der Determinante prüfen. Dazu verwenden Sie die Funktion \(Det()\).
Wenn \(Det()\) als Resultat eine Null liefert ist die Matrix singulär und kann nicht invertiert werden.
Der Wert der Determinante ist 0, wenn eine der folgenden Aussagen zutrifft
Alle Elemente einer Zeile oder Spalte sind null
Zwei Zeilen oder Spalten sind identisch
Zwei Zeilen oder Spalten sind proportional
Invm (Matrix)
English
