QR Funktion
Funktionalität zur QR Faktorisierung
Beschreibung
Die Funktion \(QR\) enthält die Funktionalität zur QR Faktorisierung einer modifizierten Gram-Schmidt-Orthogonalization.
Jede reale quadratische Matrix \(A\) kann zerlegt werden als \(A = QR\).
\(Q\) ist eine orthogonale \(m * n\) Matrix und \(R\) ist die obere Dreiecksmatrix \(n * n\)
QR ist als RedCrab Klasse implementiert. Das Resultat ist ein Objekt der Klasse QR
Syntax
QR (Matrix)
QR (Format, Matrix)
Elemente der Klasse QR
M
Q
R
Faktorisierbare Matrix
Orthogonale \(m * n\) Matrix
Obere Dreiecksmatrix
Beispiel

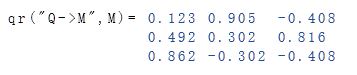
Zugriff auf Element \(Q\) per Formatstring:
|
|
Matrix Funktionen
Verbindet Matrizen oder Vektoren
Cholesky-Zerlegung einer Matrix
Liefert die Determinante einer Matrix
Generiert eine Matrix der erste Diagonale
Liefert die erste Diagonale einer Matrix
Invertiert eine quadratische Matrix
Unteres Dreieck einer Matrix
LU Faktorisierung
Generiert eine Matrix
Liefert den Wert mn einer Matrix
Matrizen Multiplikation
induzierte L1-Norm einer Matrix
induzierte L2-Norm einer Matrix
QR Faktorisierung
Rekonstruktion einer Cholesky-Zerlegung
Singulärwert Zerlegung einer Matrix
Transportierung einer Matrix
Obere Dreieck einer Matrix
XYZ Matrix Rotation
|
|
|
|