LU Funktion
Zerlegung einer regulären Matrix
Beschreibung
Die \(LU\) LU-Faktorisierung ist eine Zerlegung der regulären Matrix M in das Produkt einer linken unteren Dreiecksmatrix L und einer rechten oberen Dreiecksmatrix U. So ist A = L * U
Die Implementation verwendet eine Reihe von Pivotelemente zur Erhöhung der numerischen Stabilität. Die Pivotelemente kodieren eine Permutationsmatrix P, so dass P * A = L * U
LU ist als RedCrab Klasse implementiert. Das Resultat ist ein Objekt der Klasse LU.
Syntax
LU (Matrix)
LU (Format, Matrix)
Elemente der Klasse LU
M
U
L
P
Faktorisierungs Matrix
Liefert das obere Dreieck
Liefert das untere Dreieck
Liefert die verwendete Permutation der LU Zerlegung
Beispiel

Alternativer Zugriff auf das Element \(U\) mit einem Formatstring zur Ausgabe des oberen Dreiecks:
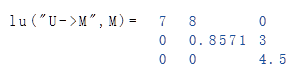
|
|
Matrix Funktionen
|
|