Kugelring

Definition, Eigenschaften und Formeln zur Berechnung eines Kugelrings

Ein Kugelring ist ein geometrischer Körper, der durch die Bohrung einer zylindrischen Höhlung durch eine Vollkugel entsteht. Er wird außen von einer symmetrischen Kugelschicht und innen von der Mantelfläche eines geraden Kreiszylinders begrenzt.

Eine besondere Eigenschaft des Kugelrings ist, dass sein Volumen nur von der Höhe \(L\) des Kugelrings abhängt und nicht vom Kugelradius \(R\). Dies ist intuitiv plausibel, da der Kugelring mit zunehmendem Kugelradius immer dünner wird.

Grundelemente des Kugelrings

Kugelradius \(R\)

Radius der ursprünglichen Kugel

Zylinderradius \(r\)

Radius der zylindrischen Bohrung

Ringbreite \(L\)

Höhe des verbleibenden Rings zwischen den Schnittebenen

Volumen

Hängt nur von \(L\) ab, nicht von \(R\)

Besondere Eigenschaften:
  • Das Volumen des Kugelrings ist unabhängig vom Kugelradius \(R\)
  • Es hängt nur von der Höhe \(L\) des Rings ab: \(V_{\text{Ring}} = \frac{\pi L^3}{6}\)
  • Je größer der Kugelradius, desto kleiner wird der Zylinderradius bei gleicher Ringbreite
  • Der Kugelring ist ein Beispiel für ein kontraintuitives geometrisches Phänomen

Visualisierung

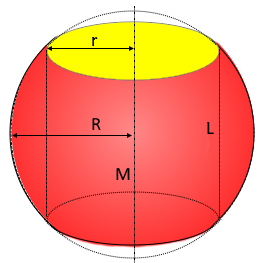
Kugelring Draufsicht

Kugelring - Draufsicht

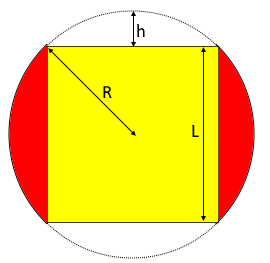
Kugelring Seitenansicht

Kugelring - Seitenansicht mit zylindrischer Bohrung

Formeln für den Kugelring

Für einen Kugelring mit Kugelradius \(R\), Zylinderradius \(r\), Ringbreite \(L\), Volumen \(V_{\text{Ring}}\) und Oberfläche \(S\):

Volumen des Kugelrings

Bemerkenswerterweise nur abhängig von der Ringbreite \(L\):

\[\displaystyle V_{\text{Ring}} = \frac{\pi L^3}{6}\]

Ringbreite \(L\)

Zusammenhang zwischen Kugelradius und Zylinderradius:

\[\displaystyle L = 2\sqrt{R^2 - r^2}\]

Kugelradius \(R\)

Aus Zylinderradius und Ringbreite:

\[\displaystyle R = \sqrt{r^2 + \left(\frac{L}{2}\right)^2}\]

Zylinderradius \(r\)

Aus Kugelradius und Ringbreite:

\[\displaystyle r = \sqrt{R^2 - \left(\frac{L}{2}\right)^2}\]

Volumen des Zylinders

Die Bohrung hat zylindrische Form:

\[\displaystyle V_{\text{Zyl}} = \pi r^2 L\]

Oberfläche des Kugelrings

Äußere Kugelschicht plus innere Zylindermantel:

\[\displaystyle S = 2\pi L(r + R)\]

Alternativ mit Kugelradius und Zylinderradius:

\[\displaystyle S = 4\pi(r + R)\sqrt{R^2 - r^2}\]

Praktische Beispiele

Beispiel 1: Volumen des Kugelrings mit gegebener Ringbreite

Gegeben: \(L = 10\,\text{cm}\) (Ringbreite)

\[\displaystyle V_{\text{Ring}} = \frac{\pi L^3}{6} = \frac{\pi \cdot 10^3}{6} = \frac{1000\pi}{6} \approx 523.60\,\text{cm}^3\]

Beachte: Das Volumen ist unabhängig vom Kugelradius \(R\)!

Beispiel 2: Kugelradius und Zylinderradius berechnen

Gegeben: \(R = 15\,\text{cm}\), \(L = 10\,\text{cm}\)

\[\displaystyle r = \sqrt{R^2 - \left(\frac{L}{2}\right)^2} = \sqrt{15^2 - 5^2} = \sqrt{225 - 25} = \sqrt{200} \approx 14.14\,\text{cm}\]
\[\displaystyle V_{\text{Ring}} = \frac{\pi \cdot 10^3}{6} \approx 523.60\,\text{cm}^3\]

Beispiel 3: Oberfläche des Kugelrings

Gegeben: \(R = 15\,\text{cm}\), \(r = 14.14\,\text{cm}\), \(L = 10\,\text{cm}\)

\[\displaystyle S = 2\pi L(r + R) = 2\pi \cdot 10 \cdot (14.14 + 15) = 20\pi \cdot 29.14 \approx 1830.97\,\text{cm}^2\]

Besondere Eigenschaften und Anwendungen

Das Invarianzphänomen des Kugelrings:
  • Das Volumen eines Kugelrings hängt NUR von der Höhe \(L\) ab
  • Ein Kugelring mit Höhe 10 cm hat das gleiche Volumen, unabhängig davon ob \(R = 10\text{ cm}\) oder \(R = 1000\text{ km}\)
  • Dies ist eines der kontraintuitivsten Ergebnisse in der Elementargeometrie
  • Historisch bekannt als "Napkin Ring Problem" in der englischsprachigen Literatur

Zusammenfassung

Definition

Kugel mit zylindrischer Bohrung durch das Zentrum

Volumen

\[\displaystyle V = \frac{\pi L^3}{6}\]
Nur von L abhängig!

Oberfläche

\[\displaystyle S = 2\pi L(r + R)\]

Ringbreite

\[\displaystyle L = 2\sqrt{R^2 - r^2}\]



Kugel
Kugelring
Kugelsegment
Kugelsektor
Kegel
Pyramide











Ist diese Seite hilfreich?            
Vielen Dank für Ihr Feedback!

Das tut uns leid

Wie können wir die Seite verbessern?