Kugelsektor - Formeln und Eigenschaften

Ein Kugelsektor (auch Kugelausschnitt genannt) ist ein kegelartiger Ausschnitt vom Mittelpunkt einer Kugel bis zu ihrer Oberfläche. Er besteht aus einem Kegel und einem Kugelsegment, die sich eine gemeinsame Basis teilen.

Der Kugelsektor wird durch den Kugelradius \(R\), die Höhe des Kugelsegments \(h\) und den Radius der Basisfläche \(a\) bestimmt. Diese drei Größen sind voneinander abhängig — der Sektor ist bereits durch zwei dieser Größen eindeutig bestimmt.

Grundelemente des Kugelsektors

Kugelradius \(R\)

Radius der ursprünglichen Kugel

Segmenthöhe \(h\)

Höhe des Kugelsegments vom Schnitt bis zur Kugelspitze

Basisradius \(a\)

Radius der kreisförmigen Basisfläche

Zentralwinkel \(\theta\)

Winkel vom Mittelpunkt zum Rand der Basisfläche

Struktur des Kugelsektors:

Besteht aus einem Kugelsegment (gekrümmter Teil) plus einem Kegel (unterer Teil)
Die drei Größen \(R\), \(h\) und \(a\) sind abhängig voneinander
Der Sektor ist durch zwei beliebige dieser Größen eindeutig bestimmt
Die Größen können ineinander umgerechnet werden

Visualisierung

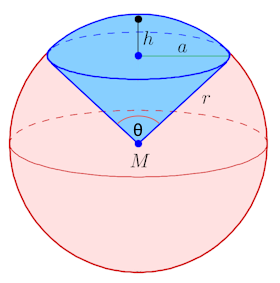
Kugelsektor mit Höhe h, Basisradius a und Kugelradius R

Formeln für den Kugelsektor

Für einen Kugelsektor mit Kugelradius \(R\), Segmenthöhe \(h\), Basisradius \(a\) und Zentralwinkel \(\theta\):

Basisradius \(a\)

Aus Kugelradius und Höhe:

\[\displaystyle a = \sqrt{2Rh - h^2}\]

Segmenthöhe \(h\)

Aus Kugelradius und Basisradius:

\[\displaystyle h = R - \sqrt{R^2 - a^2}\]

Kugelradius \(R\)

Aus Basisradius und Höhe:

\[\displaystyle R = \frac{a^2 + h^2}{2h}\]

Volumen des Kugelsektors

Mit Kugelradius und Höhe:

\[\displaystyle V = \frac{2\pi R^2 h}{3}\]

Mit Höhe und Basisradius:

\[\displaystyle V = \frac{\pi h}{6}(3a^2 + h^2)\]

Mit Zentralwinkel:

\[\displaystyle V = \frac{2\pi R^3}{3}(1 - \cos \theta)\]

Oberfläche der Kugelkappe

Mit Kugelradius und Höhe:

\[\displaystyle S_K = 2\pi Rh\]

Mit Höhe und Basisradius:

\[\displaystyle S_K = \pi(a^2 + h^2)\]

Mit Zentralwinkel:

\[\displaystyle S_K = 2\pi R^2(1 - \cos \theta)\]

Mantelfläche des Kegels

Mit Kugelradius und Höhe:

\[\displaystyle S_L = \pi a\sqrt{(2R - h)h}\]

Mit Basisradius und Höhe:

\[\displaystyle S_L = \pi \frac{a(a^2 + h^2)}{2h}\]

Mit Zentralwinkel:

\[\displaystyle S_L = \pi R^2 \sin \theta\]

Gesamtoberfläche des Kugelsektors

Kappe plus Kegelmantelfläche:

\[\displaystyle S_{\text{Sek}} = S_K + S_L\]

Alternative Form:

\[\displaystyle S_{\text{Sek}} = \pi R(a + 2h)\]

Mit Zentralwinkel:

\[\displaystyle S_{\text{Sek}} = \pi R^2(2 - 2\cos \theta + \sin \theta)\]

Praktische Beispiele

Beispiel 1: Volumen mit Kugelradius und Höhe

Gegeben: \(R = 25\,\text{cm}\), \(h = 15\,\text{cm}\)

\[\displaystyle V = \frac{2\pi R^2 h}{3} = \frac{2\pi \cdot 25^2 \cdot 15}{3} = \frac{18750\pi}{3} = 6250\pi \approx 19634.95\,\text{cm}^3\]

Beispiel 2: Basisradius berechnen

Gegeben: \(R = 20\,\text{cm}\), \(h = 10\,\text{cm}\)

\[\displaystyle a = \sqrt{2Rh - h^2} = \sqrt{2 \cdot 20 \cdot 10 - 10^2} = \sqrt{400 - 100} = \sqrt{300} \approx 17.32\,\text{cm}\]

Beispiel 3: Kappe und Kegelmantelfläche

Gegeben: \(R = 30\,\text{cm}\), \(h = 12\,\text{cm}\)

\[\displaystyle S_K = 2\pi Rh = 2\pi \cdot 30 \cdot 12 = 720\pi \approx 2262.74\,\text{cm}^2\]

Mit \(a = \sqrt{2 \cdot 30 \cdot 12 - 12^2} = \sqrt{576} = 24\,\text{cm}\):

\[\displaystyle S_L = \pi \frac{a(a^2 + h^2)}{2h} = \pi \frac{24(576 + 144)}{24} = \pi \cdot 720 \approx 2262.74\,\text{cm}^2\]

Beispiel 4: Gesamtoberfläche

Mit den Werten aus Beispiel 3:

\[\displaystyle S_{\text{Sek}} = \pi R(a + 2h) = \pi \cdot 30(24 + 24) = 1440\pi \approx 4525.47\,\text{cm}^2\]

Wichtige Beziehungen

Geometrische Zusammenhänge:

Basisradius und Höhe sind durch \(a^2 = 2Rh - h^2\) verbunden
Der Kegelmantelfläche \(S_L = \pi a \cdot l\) wobei \(l\) die Seitenlänge des Kegels ist
\(l = \sqrt{a^2 + (R-h)^2}\) ist die Seitenlänge des Kegels
Für kleine \(h\) (flacher Sektor) ist \(V \approx \frac{2\pi R^2 h}{3}\)
Die Gesamtoberfläche teilt sich in Kappe und Kegelmantel: \(S_{\text{Sek}} = S_K + S_L\)

Zusammenfassung

Definition

Kugelsegment + Kegel mit gemeinsamer Basisfläche

Volumen

\[\displaystyle V = \frac{2\pi R^2 h}{3}\]

Kappe-Fläche

\[\displaystyle S_K = 2\pi Rh\]

Gesamtfläche

\[\displaystyle S_{\text{Sek}} = \pi R(a + 2h)\]

Kugelsektor online berechnen