Kegel - Formeln und Eigenschaften

Ein Kegel ist ein dreidimensionaler geometrischer Körper, der sich von einer flachen, kreisförmigen Basis (Grundfläche) zu einem Punkt verjüngt, der als Spitze oder Scheitelpunkt bezeichnet wird.

Der Kegel ist eine der fundamentalsten 3D-Formen mit vielen praktischen Anwendungen in Mathematik, Physik und Ingenieurwesen.

Grundelemente des Kegels

Grundflächenradius \(r\)

Radius der kreisförmigen Basis

Höhe \(h\)

Senkrechte Entfernung von der Basis zur Spitze

Mantellinie \(L\)

Geradliniger Abstand von der Basiskante zur Spitze

Kegel-Typ

Gerade (Spitze über Mittelpunkt) oder schief (Spitze versetzt)

Wichtige Eigenschaften:

Die Basis ist immer eine Kreisfläche (bei einem geraden Kegel)
Die Mantelfläche ist eine gekrümmte Fläche, die sich zur Spitze verjüngt
Liegt die Spitze über dem Mittelpunkt der Basis, ist der Kegel gerade
Weicht die Spitze ab, spricht man von einem schiefen Kegel
Die Mantellinie, Höhe und Radius sind durch den Satz des Pythagoras verbunden

Visualisierung

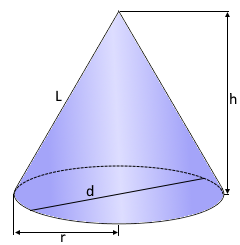
Gerader Kegel mit Höhe h, Grundflächenradius r und Mantellinie L

Formeln für den geraden Kegel

Für einen geraden Kegel mit Grundflächenradius \(r\), Höhe \(h\), Mantellinie \(L\), Grundfläche \(A\), Mantelfläche \(S_M\), Oberfläche \(S\) und Volumen \(V\):

Grundflächenradius \(r\)

Aus der Grundfläche:

\[\displaystyle r = \sqrt{\frac{A}{\pi}}\]

Durchmesser \(d\)

\[\displaystyle d = 2r = 2\sqrt{\frac{A}{\pi}}\]

Grundfläche \(A\)

\[\displaystyle A = \pi r^2\]

Mantellinie \(L\)

Mit Höhe und Radius (Satz des Pythagoras):

\[\displaystyle L = \sqrt{h^2 + r^2}\]

Höhe \(h\)

Aus Mantellinie und Radius:

\[\displaystyle h = \sqrt{L^2 - r^2}\]

Aus Volumen und Grundfläche:

\[\displaystyle h = \frac{3V}{A} = \frac{3V}{\pi r^2}\]

Mantelfläche

Mit Radius und Mantellinie:

\[\displaystyle S_M = \pi r L\]

Mit Umfang und Mantellinie:

\[\displaystyle S_M = \frac{U \cdot L}{2} = \frac{2\pi r \cdot L}{2} = \pi r L\]

Oberfläche

Mantelfläche plus Grundfläche:

\[\displaystyle S = S_M + A = \pi r L + \pi r^2 = \pi r(L + r)\]

Volumen

Mit Grundfläche und Höhe:

\[\displaystyle V = \frac{A \cdot h}{3} = \frac{\pi r^2 h}{3}\]

Praktische Beispiele

Beispiel 1: Volumen und Oberfläche mit Radius und Höhe

Gegeben: \(r = 8\,\text{cm}\), \(h = 15\,\text{cm}\)

\[\displaystyle L = \sqrt{h^2 + r^2} = \sqrt{15^2 + 8^2} = \sqrt{225 + 64} = \sqrt{289} = 17\,\text{cm}\]

\[\displaystyle V = \frac{\pi r^2 h}{3} = \frac{\pi \cdot 8^2 \cdot 15}{3} = \frac{960\pi}{3} = 320\pi \approx 1005.31\,\text{cm}^3\]

\[\displaystyle S = \pi r(L + r) = \pi \cdot 8(17 + 8) = 200\pi \approx 628.32\,\text{cm}^2\]

Beispiel 2: Höhe aus Mantellinie und Radius

Gegeben: \(L = 25\,\text{cm}\), \(r = 7\,\text{cm}\)

\[\displaystyle h = \sqrt{L^2 - r^2} = \sqrt{25^2 - 7^2} = \sqrt{625 - 49} = \sqrt{576} = 24\,\text{cm}\]

Beispiel 3: Mantelfläche berechnen

Gegeben: \(r = 6\,\text{cm}\), \(L = 10\,\text{cm}\)

\[\displaystyle S_M = \pi r L = \pi \cdot 6 \cdot 10 = 60\pi \approx 188.50\,\text{cm}^2\]

Beispiel 4: Volumen aus Grundfläche und Höhe

Gegeben: \(A = 78.54\,\text{cm}^2\) (entspricht \(r = 5\,\text{cm}\)), \(h = 12\,\text{cm}\)

\[\displaystyle V = \frac{A \cdot h}{3} = \frac{78.54 \cdot 12}{3} = \frac{942.48}{3} = 314.16\,\text{cm}^3\]

Wichtige Beziehungen und Besonderheiten

Geometrische Zusammenhänge:

Mantellinie, Höhe und Radius bilden ein rechtwinkliges Dreieck: \(L^2 = h^2 + r^2\)
Das Volumen eines Kegels ist genau ein Drittel des Volumens eines Zylinders mit gleicher Basis und Höhe
\(V_{\text{Kegel}} = \frac{1}{3} V_{\text{Zylinder}} = \frac{1}{3} \pi r^2 h\)
Die Mantelfläche ist immer kleiner als die Grundfläche (außer bei sehr flachen Kegeln)
Der Öffnungswinkel \(\alpha\) erfüllt: \(\sin \alpha = \frac{r}{L}\) und \(\cos \alpha = \frac{h}{L}\)

Zusammenfassung

Definition

Geometrischer Körper mit kreisförmiger Basis und einer Spitze

Volumen

\[\displaystyle V = \frac{\pi r^2 h}{3}\]

Oberfläche

\[\displaystyle S = \pi r(L + r)\]

Mantellinie

\[\displaystyle L = \sqrt{h^2 + r^2}\]

Kegel online berechnen