Kugelsegment

Definition, Eigenschaften und Formeln zur Berechnung eines Kugelsegments

Ein Kugelsegment (auch Kugelabschnitt genannt) ist ein Teil einer Kugel, der durch den Schnitt mit einer oder zwei parallelen Ebenen abgetrennt wird.

Ein Kugelsegment hat die Form einer Kuppel und besitzt als Grundfläche eine Kreisscheibe. Der gekrümmte Teil der Oberfläche eines Kugelsegments wird Kugelkalotte oder Kugelkappe genannt. Eine Halbkugel ist ein Sonderfall eines Kugelsegments, bei dem der Schnitt durch den Mittelpunkt der Kugel diese in zwei gleich große Hälften teilt.

Grundelemente des Kugelsegments

Kugelradius \(R\)

Radius der ursprünglichen Kugel

Segmenthöhe \(h\)

Höhe des Segments vom Schnitt bis zum höchsten Punkt

Segmentradius \(a\)

Radius der kreisförmigen Grundfläche des Segments

Kalottenwinkel \(\theta\)

Zentralwinkel des Segments vom Mittelpunkt aus

Besonderheiten:
  • Das Kugelsegment wird durch Radius \(R\), Höhe \(h\) und Segmentradius \(a\) bestimmt
  • Bei \(h = R\) erhält man eine Halbkugel
  • Der Kugelkappe-Radius hängt geometrisch von \(R\), \(h\) und \(a\) ab
  • Es gibt verschiedene äquivalente Formeln je nach gegebenen Größen

Visualisierung

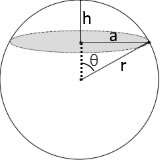
Kugelsegment

Kugelsegment mit Höhe h, Segmentradius a und Kugelradius R

Formeln für das Kugelsegment

Für ein Kugelsegment mit Kugelradius \(R\), Segmenthöhe \(h\), Segmentradius \(a\) und Zentralwinkel \(\theta\):

Volumen des Segments

Mit Höhe und Kugelradius:

\[\displaystyle V_s = \frac{\pi h^2}{3}(3R - h)\]

Mit Höhe und Segmentradius:

\[\displaystyle V_s = \frac{\pi h}{6}(3a^2 + h^2)\]

Segmenthöhe \(h\)

Aus Kugelradius und Segmentradius:

\[\displaystyle h = R - \sqrt{R^2 - a^2}\]

Segmentradius \(a\)

Aus Kugelradius und Segmenthöhe:

\[\displaystyle a = \sqrt{2Rh - h^2}\]

Oberfläche der Kugelkappe

Mit Höhe und Kugelradius:

\[\displaystyle S_{\text{Kappe}} = 2\pi Rh\]

Mit Höhe und Segmentradius:

\[\displaystyle S_{\text{Kappe}} = \pi(a^2 + h^2)\]

Basisfläche des Segments

Kreisfläche mit Segmentradius \(a\):

\[\displaystyle A_{\text{Basis}} = \pi a^2\]

Gesamtoberfläche des Segments

Kappe plus Basisfläche:

\[\displaystyle S_s = \pi(2Rh + a^2)\]

Alternative Formel mit nur Höhe:

\[\displaystyle S_s = \pi h(4R - h)\]

Kugelradius \(R\)

Aus Segmentradius und Höhe:

\[\displaystyle R = \frac{a^2 + h^2}{2h}\]

Praktische Beispiele

Beispiel 1: Volumen mit Höhe und Radius

Gegeben: \(R = 20\,\text{cm}\), \(h = 10\,\text{cm}\)

\[\displaystyle V_s = \frac{\pi h^2}{3}(3R - h) = \frac{\pi \cdot 10^2}{3}(3 \cdot 20 - 10)\]
\[\displaystyle = \frac{100\pi}{3} \cdot 50 = \frac{5000\pi}{3} \approx 5236.0\,\text{cm}^3\]

Beispiel 2: Segmentradius berechnen

Gegeben: \(R = 15\,\text{cm}\), \(h = 8\,\text{cm}\)

\[\displaystyle a = \sqrt{2Rh - h^2} = \sqrt{2 \cdot 15 \cdot 8 - 8^2} = \sqrt{240 - 64} = \sqrt{176} \approx 13.27\,\text{cm}\]

Beispiel 3: Oberfläche der Kappe

Gegeben: \(R = 25\,\text{cm}\), \(h = 12\,\text{cm}\)

\[\displaystyle S_{\text{Kappe}} = 2\pi Rh = 2\pi \cdot 25 \cdot 12 = 600\pi \approx 1884.96\,\text{cm}^2\]

Beispiel 4: Sonderfall Halbkugel

Für \(h = R = 10\,\text{cm}\) (Halbkugel):

\[\displaystyle V_s = \frac{\pi \cdot 10^2}{3}(3 \cdot 10 - 10) = \frac{100\pi}{3} \cdot 20 = \frac{2000\pi}{3} \approx 2094.4\,\text{cm}^3\]

Wichtige Beziehungen

Geometrische Beziehungen:
  • Der Segmentradius \(a\) und die Höhe \(h\) sind durch \(a^2 + (R-h)^2 = R^2\) verbunden
  • Dies ergibt: \(a = \sqrt{2Rh - h^2}\)
  • Bei \(h = 0\) ist \(a = 0\) (Punkt), bei \(h = 2R\) ist das Segment die ganze Kugel
  • Für eine Halbkugel ist \(h = R\) und \(a = R\)
  • Die Oberfläche der Kappe ist \(S = 2\pi Rh\) — linear in beiden Größen

Zusammenfassung

Definition

Kugelabschnitt durch Schnitt mit Ebene(n)

Volumen

\[\displaystyle V = \frac{\pi h^2}{3}(3R - h)\]

Kappe-Fläche

\[\displaystyle S = 2\pi Rh\]

Segmentradius

\[\displaystyle a = \sqrt{2Rh - h^2}\]

Kugelsegment


Kugel
Kugelring
Kugelsegment
Kugelsektor
Kegel
Pyramide











Ist diese Seite hilfreich?            
Vielen Dank für Ihr Feedback!

Das tut uns leid

Wie können wir die Seite verbessern?