Kugelring Rechner
Rechner und Formeln zur Berechnung eines Kugelrings
Kugelring Rechner
Der Kugelring
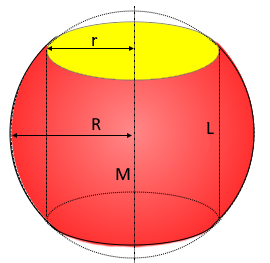
Der Kugelring ist eine Vollkugel mit einer zylindrischen Bohrung durch den Mittelpunkt.
Kugelring Eigenschaften
Der Kugelring: Kombination aus sphärischer und zylindrischer Geometrie
Kugelring Visualisierung
Der Kugelring
Vollkugel mit zylindrischer Bohrung
Kombination aus Kugel und Zylinder.
Außen gekrümmt, innen gerade.
|
|
Was ist ein Kugelring?
Der Kugelring ist ein spezieller geometrischer Körper:
- Definition: Vollkugel mit zylindrischer Bohrung durch den Mittelpunkt
- Außenfläche: Symmetrische Kugelschicht (sphärisch)
- Innenfläche: Mantelfläche eines geraden Kreiszylinders
- Hybridform: Kombination aus Kugel- und Zylindergeometrie
- Anwendung: Technik, Architektur, Physik
- Besonderheit: Komplexe Oberflächenberechnung
Geometrische Eigenschaften des Kugelrings
Der Kugelring zeigt hybride geometrische Eigenschaften:
Grundparameter
- Kugelradius R: Radius der ursprünglichen Vollkugel
- Zylinderradius r: Radius der zylindrischen Bohrung
- Zylinderhöhe L: Höhe der Bohrung (2√(R²-r²))
- Bedingung: r < R (Bohrung muss kleiner als Kugel sein)
Besondere Eigenschaften
- Hybride Oberfläche: Sphärisch außen, zylindisch innen
- Komplexes Volumen: Abhängig von L³ (nicht R³)
- Rotationssymmetrie: Um die Achse der Bohrung
- Variable Form: Von dünnem Ring bis dicker Schale
Mathematische Beziehungen des Kugelrings
Der Kugelring folgt komplexen mathematischen Gesetzen:
Volumen-Formel
Das Ringvolumen hängt von L³ ab. Überraschend einfache Formel für komplexe Geometrie.
Oberflächen-Formel
Die Oberfläche berücksichtigt beide Radien. Innen- und Außenfläche zusammen.
Anwendungen des Kugelrings
Kugelringe finden Anwendung in verschiedenen Bereichen:
Maschinenbau & Technik
- Lager und Buchsen
- Hohlkugeln mit Bohrungen
- Strömungstechnik
- Präzisionsmechanik
Physik & Chemie
- Hohlkugel-Experimente
- Strömungsmechanik
- Materialwissenschaft
- Quantenmechanik
Architektur & Design
- Skulpturale Elemente
- Moderne Architektur
- Produktdesign
- Kunstobjekte
Mathematik & CAD
- Volumenberechnung
- CAD-Konstruktion
- 3D-Modellierung
- Finite Elemente
Formeln zum Kugelring
Zylinderhöhe (L)
Höhe der zylindrischen Bohrung
Ringvolumen (VR)
Volumen des Kugelrings (ohne Bohrung)
Zylindervolumen (VC)
Volumen der zylindrischen Bohrung
Ringoberfläche (S)
Innen- und Außenoberfläche zusammen
Geometrische Beziehungen
\(r < R\)
\(L_{max} = 2R\) (bei r = 0)
\(L = 0\) (bei r = R)
Der Zylinderradius muss kleiner als der Kugelradius sein
Berechnungsbeispiel für einen Kugelring
Gegeben
Gesucht: Alle Parameter des Kugelrings
1. Zylinderhöhen-Berechnung
Für R = 8 cm, r = 6 cm:
\[L = 2 \cdot \sqrt{R^2 - r^2}\] \[L = 2 \cdot \sqrt{64 - 36} = 2 \cdot \sqrt{28}\] \[L = 2 \cdot 5.29 ≈ 10.58 \text{ cm}\]Die Zylinderhöhe beträgt etwa 10.58 cm
2. Ringvolumen-Berechnung
Mit L ≈ 10.58 cm:
\[V_R = \frac{π \cdot L^3}{6}\] \[V_R = \frac{π \cdot (10.58)^3}{6}\] \[V_R = \frac{π \cdot 1184.5}{6} ≈ 620.03 \text{ cm}^3\]Das Ringvolumen beträgt etwa 620.03 cm³
3. Zylindervolumen-Berechnung
Mit L ≈ 10.58 cm, r = 6 cm:
\[V_C = π \cdot L \cdot r^2\] \[V_C = π \cdot 10.58 \cdot 36\] \[V_C ≈ 1194.6 \text{ cm}^3\]Das Zylindervolumen beträgt etwa 1194.6 cm³
4. Ringoberflächen-Berechnung
Mit L ≈ 10.58 cm:
\[S = 2π \cdot L \cdot (r + R)\] \[S = 2π \cdot 10.58 \cdot (6 + 8)\] \[S = 2π \cdot 10.58 \cdot 14 ≈ 929.2 \text{ cm}^2\]Die Ringoberfläche beträgt etwa 929.2 cm²
5. Zusammenfassung
Der Kugelring mit R=8cm, r=6cm
6. Vergleich mit Vollkugel
VR = 620.03 cm³
V = 2144.66 cm³
Der Ring hat etwa 29% des Vollkugel-Volumens
7. Geometrische Verhältnisse
6/8 = 0.75
10.58/8 ≈ 1.32
R - r = 2 cm
Dicker Ring
Bei r/R = 0.75 entsteht ein relativ dicker Kugelring
Der Kugelring: Hybridgeometrie aus Kugel und Zylinder
Der Kugelring ist ein faszinierender geometrischer Körper, der die Eleganz der Kugelgeometrie mit der Präzision zylindrischer Formen verbindet. Als Vollkugel mit einer zylindrischen Bohrung durch den Mittelpunkt zeigt er einzigartige mathematische Eigenschaften, die ihn sowohl für theoretische Studien als auch für praktische Anwendungen interessant machen. Der Kugelring verkörpert die perfekte Synthese zwischen sphärischer Außenhülle und zylindrischer Innenstruktur, was zu überraschend eleganten Formeln führt.
Die Geometrie der Hybridform
Der Kugelring zeigt die Faszination geometrischer Kombinationen:
- Sphärische Außenhülle: Erhalt der ursprünglichen Kugeloberfläche
- Zylindrische Bohrung: Gerade, kreisförmige Durchbohrung
- Komplexe Oberfläche: Kombination aus gekrümmten und geraden Flächen
- Überraschende Volumenformel: V = π·L³/6 abhängig von Höhe L
- Radiusabhängigkeit: Höhe L = 2√(R²-r²) bestimmt alle Eigenschaften
- Rotationssymmetrie: Um die Achse der zylindrischen Bohrung
- Variable Geometrie: Von dünnem Ring bis dicker Schale
Mathematische Eleganz
Überraschende Formeln
Die Volumenformel V = π·L³/6 ist überraschend einfach und hängt nur von der Höhe L ab, nicht direkt von den Radien R und r.
Hybride Oberfläche
Die Oberflächenformel S = 2π·L·(r+R) berücksichtigt elegant beide Radien und zeigt die Kombination aus Innen- und Außenfläche.
Praktische Relevanz
In Maschinenbau und Technik bietet der Kugelring optimale Lösungen für Lager, Buchsen und Hohlkugel-Konstruktionen.
Geometrische Grenzen
Die Bedingung r < R definiert die Existenz des Kugelrings, bei r = R verschwindet die Höhe L und damit der Ring.
Zusammenfassung
Der Kugelring verkörpert die perfekte Harmonie zwischen sphärischer und zylindrischer Geometrie. Als Vollkugel mit zylindrischer Bohrung vereint er die natürliche Eleganz der Kugelform mit der konstruktiven Klarheit zylindrischer Strukturen. Seine mathematischen Eigenschaften - mit der überraschenden Volumenformel π·L³/6 und der eleganten Oberflächenberechnung - machen ihn zu einem faszinierenden Studienobjekt der Geometrie. Von technischen Anwendungen in Lagern und Buchsen über physikalische Experimente mit Hohlkugeln bis hin zu architektonischen Elementen bietet der Kugelring vielseitige Lösungen für komplexe dreidimensionale Probleme. Er demonstriert eindrucksvoll, wie die Kombination verschiedener geometrischer Grundformen zu neuen, überraschenden mathematischen Beziehungen führt und dabei sowohl theoretische Schönheit als auch praktischen Nutzen vereint.
|
|
|
|