Kugelsektor Rechner
Onlinerechner und Formeln zur Berechnung eines Kugelsektors
Kugelsektor Rechner
Der Kugelsektor
Der Kugelsektor ist ein kegelartiger Ausschnitt vom Mittelpunkt einer Kugel bis zu ihrer Oberfläche.
Kugelsektor Eigenschaften
Der Kugelsektor: Kombination aus Kugelsegment und Kegel
Kugelsektor Visualisierung
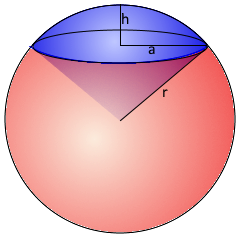
Der Kugelsektor
Kegelartiger Ausschnitt vom Mittelpunkt
Vollständiger Ausschnitt vom Zentrum.
Kombination aus Segment und Kegel.
|
|
Was ist ein Kugelsektor?
Der Kugelsektor ist ein spezieller geometrischer Körper:
- Definition: Kegelartiger Ausschnitt vom Mittelpunkt einer Kugel zur Oberfläche
- Struktur: Kombination aus Kugelsegment und Kegel
- Vollständigkeit: Reicht vom Zentrum bis zur Kugeloberfläche
- Besonderheit: Vereint gekrümmte und gerade Flächen
- Anwendung: Optik, Geometrie, Architektur
- Beziehung: Erweitert das Kugelsegment zum Mittelpunkt
Geometrische Eigenschaften des Kugelsektors
Der Kugelsektor zeigt hybride geometrische Eigenschaften:
Grundparameter
- Kugelradius r: Radius der ursprünglichen Vollkugel
- Segmenthöhe h: Höhe des Kugelsegment-Anteils
- Segmentradius a: Radius der kreisförmigen Schnittfläche
- Mittelpunkt: Ausgangspunkt der kegelartigen Erweiterung
Besondere Eigenschaften
- Hybride Form: Kugelsegment plus Kegelmantel
- Vollständiger Ausschnitt: Vom Zentrum zur Oberfläche
- Kegelartige Erweiterung: Natürliche Fortsetzung zum Mittelpunkt
- Rotationssymmetrie: Um die Achse durch den Mittelpunkt
Mathematische Beziehungen des Kugelsektors
Der Kugelsektor folgt erweiterten mathematischen Gesetzen:
Volumen-Formel
Das Volumen ist proportional zu r² und h. Einfachere Formel als beim Kugelsegment.
Oberflächen-Formel
Die Oberfläche kombiniert Kugelkappe und konischen Mantel.
Anwendungen des Kugelsektors
Kugelsektoren finden Anwendung in verschiedenen Bereichen:
Optik & Photonik
- Linsensegmente
- Reflektoren
- Strahlenoptik
- Beleuchtungstechnik
Geodäsie & Navigation
- Erdkugel-Sektoren
- Koordinatensysteme
- Satellitennavigation
- Vermessungstechnik
Architektur & Design
- Spezielle Kuppelformen
- Moderne Architektur
- Skulpturale Elemente
- Innenraumgestaltung
Mathematik & Physik
- Volumenberechnungen
- Integralrechnung
- Geometrische Studien
- Raumgeometrie
Formeln zum Kugelsektor
Sektor Volumen (Vs)
Volumen des kegelartigen Sektors
Segment Höhe (h)
Höhe aus Kugel- und Segmentradius
Segmentradius (a)
Radius der kreisförmigen Schnittfläche
Kugelradius (r)
Rekonstruktion des Kugelradius
Oberfläche der Kappe (Sc)
Gekrümmte Oberfläche der Kugelkappe
Oberfläche des Kegels (SL)
Kegelmantel vom Mittelpunkt zur Schnittfläche
Oberfläche des Sektors (S)
Kugelkappe plus Kegeloberfläche
Wichtiger Unterschied zum Kugelsegment
Der Kugelsektor entspricht einem Kugelsegment, das statt der flachen Grundfläche eine kegelartige Fortsetzung zum Mittelpunkt der Kugel hat. Dadurch entsteht ein vollständiger, geschlossener Körper vom Zentrum bis zur Kugeloberfläche.
Berechnungsbeispiel für einen Kugelsektor
Gegeben
Gesucht: Alle Parameter des Kugelsektors
1. Segmentradius-Berechnung
Für r = 12 cm, h = 5 cm:
\[a = \sqrt{r^2 - (r - h)^2}\] \[a = \sqrt{144 - (12 - 5)^2}\] \[a = \sqrt{144 - 49} = \sqrt{95} ≈ 9.75 \text{ cm}\]Der Segmentradius beträgt etwa 9.75 cm
2. Sektor-Volumen-Berechnung
Mit r = 12 cm, h = 5 cm:
\[V_s = \frac{2π \cdot r^2 \cdot h}{3}\] \[V_s = \frac{2π \cdot 144 \cdot 5}{3}\] \[V_s = \frac{1440π}{3} = 480π ≈ 1507.96 \text{ cm}^3\]Das Sektorvolumen beträgt etwa 1507.96 cm³
3. Kappenoberflächen-Berechnung
Mit r = 12 cm, h = 5 cm:
\[S_c = 2π \cdot r \cdot h\] \[S_c = 2π \cdot 12 \cdot 5\] \[S_c = 120π ≈ 377.0 \text{ cm}^2\]Die Kappenoberfläche beträgt etwa 377.0 cm²
4. Kegeloberflächen-Berechnung
Mit a ≈ 9.75 cm, r = 12 cm:
\[S_L = π \cdot a \cdot r\] \[S_L = π \cdot 9.75 \cdot 12\] \[S_L = 117π ≈ 367.6 \text{ cm}^2\]Die Kegeloberfläche beträgt etwa 367.6 cm²
5. Gesamtoberflächen-Berechnung
Kappe plus Kegel:
\[S = S_c + S_L\] \[S = 377.0 + 367.6\] \[S ≈ 744.6 \text{ cm}^2\]Die Gesamtoberfläche beträgt etwa 744.6 cm²
6. Zusammenfassung
Der Kugelsektor mit 5 cm Segmenthöhe
7. Vergleich mit Kugelsegment
V = 1507.96 cm³
V ≈ 1272.35 cm³
≈ 235.61 cm³
Der Sektor hat durch den Kegel etwa 18.5% mehr Volumen als das Segment
8. Geometrische Analyse
h/r = 5/12 ≈ 0.42
a/r = 9.75/12 ≈ 0.81
Mittlere Höhe
Weite Basis
Bei h/r ≈ 0.42 entsteht ein ausgewogener Kugelsektor mit weiter Öffnung
Der Kugelsektor: Vollständige Kegelgeometrie
Der Kugelsektor ist ein faszinierender geometrischer Körper, der die Eleganz des Kugelsegments mit der Vollständigkeit einer kegelartigen Erweiterung zum Mittelpunkt verbindet. Als vollständiger Ausschnitt vom Zentrum einer Kugel bis zu ihrer Oberfläche zeigt er die perfekte Synthese zwischen sphärischer Krümmung und konischer Geometrie. Seine mathematischen Eigenschaften - mit der eleganten Volumenformel V = 2πr²h/3 und der hybriden Oberflächenberechnung - machen ihn zu einem idealen Beispiel für komplexe dreidimensionale Geometrie. Der Kugelsektor demonstriert, wie aus der Erweiterung einer bekannten Form neue, praktisch relevante Körper entstehen.
Die Geometrie der Vollständigkeit
Der Kugelsektor zeigt die Perfektion vollständiger Ausschnitte:
- Kegelartige Erweiterung: Natürliche Fortsetzung des Kugelsegments zum Mittelpunkt
- Hybride Oberfläche: Kombination aus Kugelkappe und Kegelmantel
- Vollständiger Körper: Geschlossene Form vom Zentrum zur Oberfläche
- Elegante Mathematik: Einfachere Volumenformel als beim Kugelsegment
- Rotationssymmetrie: Perfekte Symmetrie um die zentrale Achse
- Skalierbare Geometrie: Von spitzem Kegel bis zu breiten Sektoren
- Praktische Relevanz: Wichtig in Optik, Navigation und Architektur
Mathematische Eleganz
Volumen-Vereinfachung
Die Volumenformel V = 2πr²h/3 ist eleganter als beim Kugelsegment und zeigt die direkte Proportionalität zu r² und h.
Oberflächen-Hybridität
Die Kombination aus Kugelkappe (2πrh) und Kegelmantel (πar) zeigt die duale Natur des Sektors.
Optische Anwendungen
In der Optik ermöglichen Kugelsektoren präzise Strahlführung und Lichtbündelung durch ihre kegelartige Geometrie.
Geodätische Bedeutung
In der Geodäsie helfen Kugelsektoren bei der Berechnung von Erdkugel-Ausschnitten und Koordinatensystemen.
Zusammenfassung
Der Kugelsektor verkörpert die perfekte Vollendung des Kugelsegments durch seine kegelartige Erweiterung zum Mittelpunkt. Als vollständiger Ausschnitt vom Zentrum einer Kugel bis zu ihrer Oberfläche vereint er die natürliche Eleganz sphärischer Krümmung mit der konstruktiven Klarheit konischer Geometrie. Seine mathematischen Eigenschaften - von der vereinfachten Volumenformel bis zur hybriden Oberflächenberechnung - demonstrieren die Schönheit erweiternder Geometrie. Von optischen Anwendungen in der Beleuchtungstechnik über geodätische Berechnungen in der Vermessungstechnik bis hin zu architektonischen Sonderlösungen zeigt der Kugelsektor seine vielseitige Anwendbarkeit. Er verbindet die Reinheit geometrischer Formen mit der Funktionalität vollständiger Körper und bleibt ein eindrucksvolles Beispiel für die Kraft mathematischer Erweiterungen in der dreidimensionalen Geometrie.
|
|
|
|