Internal Resistance Calculator
Online calculator for determining the internal resistance of a voltage source
Calculation
|
|
Good to know
What is internal resistance?
The internal resistance of a voltage source can be calculated by comparing two different load conditions. The open-circuit voltage and the loaded voltage are measured.
Circuit diagram
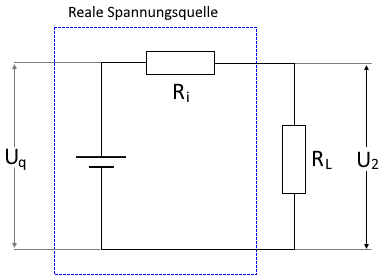
Voltage source with internal resistance and load resistance
Basic formulas
Variables
|
|
Formulas for internal resistance
When a consumer is connected to an electrical source (e.g. a battery), a current flows, the strength of which essentially depends on the voltage of the battery and the value of the consumer's resistance. The smaller the resistance value, the greater the current flowing in the circuit. However, there is an upper limit to the current. This limit is determined by the internal resistance of the battery.
The internal resistance can be calculated using two load conditions. First, the unloaded battery voltage (open-circuit voltage or source voltage) is measured. Then the battery is loaded with a resistor. The loaded voltage is then measured. The current can be measured or calculated using the formula below.
Current calculation
The current for a loaded power source can be calculated using the following formula:
Internal resistance
The internal resistance can then be calculated using the current and the voltage difference:
Practical example
Example: Battery internal resistance
Suppose we have a battery with an open-circuit voltage of 12 V. When the battery supplies a current of 2 A to a consumer, the voltage drops to 10 V.
Given:
- \(U_q = 12 \text{ V}\)
- \(U_2 = 10 \text{ V}\)
- \(I = 2 \text{ A}\)
Calculation:
The internal resistance of the battery is therefore 1 Ω.
Other important formulas
Terminal voltage
The terminal voltage is the measured voltage under load.
Short-circuit current
Theoretical maximum current in the event of a short circuit.
Variable legend
|
|
Battery Capacity • Capacitor Capacitance • Decibel, votage, power converter • Decibel - factor converter • Electric Power • Electric Energy • Electric Charge • Electrostatic force, Coulombs Law • Internal resistance of a power source • Ohm's law and power • Table of temperature coefficients • Temperature drift of resistance • Voltage drop • Wire resistance •