Calculate RC Parallel Circuit

Calculator and formulas for calculation of current and power of an RC parallel circuit

RC Parallel Circuit

RC Parallel Circuit

The calculator computes current, power, apparent and reactive resistance in the parallel connection of a resistor and a capacitor.

Results
Reactance XC:
Total Resistance Z:
Resistor Current IR:
Capacitor Current IC:
Total Current I:
Phase Angle φ:
Active Power P:
Reactive Power Q:
Apparent Power S:

Circuit Diagram

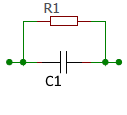
RC Parallel Circuit
Parallel Circuit Properties
  • Same voltage across all components
  • Total current is the sum of the branch currents
  • Total impedance is less than the smallest individual resistance
  • Phase shift between branch currents
Basic Formulas
\[I=\sqrt{I_R^2+I_C^2}\] \[Z=\frac{X_C \cdot R}{\sqrt{R^2+X_C^2}}\]

Total current and impedance of the RC parallel circuit.

Powers
  • Active Power P: Only in the resistor
  • Reactive Power Q: Only in the capacitor
  • Apparent Power S: Geometric sum

RC Parallel Circuit - Theory and Formulas

Basics of the RC Parallel Circuit

The total resistance of the RC parallel circuit in AC is called apparent resistance or impedance Z. Ohm's law applies to the entire circuit. In the ohmic resistor, current and voltage are in phase. In the capacitive reactance of the capacitor, the voltage lags the current by −90°.

Formulas and Calculations

Current Triangle
\[I=\sqrt{I_R^2+I_C^2}\]
ITotal current
IRCurrent through resistor
ICCurrent through capacitor
Admittance Triangle
\[Y=\sqrt{G^2+B_C^2}\]
GConductance [1/R]
BCSusceptance [1/XC]
YAdmittance [1/Z]
Impedance Triangle
\[Z=\frac{X_C \cdot R}{\sqrt{R^2+X_C^2}}\]
XCCapacitive reactance
RResistance
ZImpedance

Power Calculation

Active Power
\[P=U \cdot I_R\]

The active power is only dissipated in the resistor and converted to heat.

Reactive Power
\[Q=U \cdot I_C\]

The reactive power oscillates between the capacitor and the generator.

Apparent Power
\[S=\sqrt{P^2+Q^2}\]

The apparent power is a purely mathematical quantity.

Special Features of the Parallel Circuit

Important Properties
  • The total current is the geometric sum of the branch currents
  • The voltage is the same across all components
  • The total resistance is less than the smallest individual resistance
  • The branch currents form a right triangle
  • Admittances are used in parallel circuits
  • The phase shift between current and voltage depends on frequency

Practical Applications

Power Factor Correction:
• Compensation of inductances
• Improving cos φ
• Reducing reactive current
• Energy efficiency
Filter Applications:
• High-pass filters
• Crossovers
• Audio technology
• Signal conditioning
Oscillators:
• RC oscillators
• Phase shifters
• Frequency generators
• Clock generators


Capacitor functions

Series connection with capacitors  •  Series connection with 2 capacitors  •  Reactance Xc of a capacitor  •  Time constant of an R/C circuit  •  Capacitor charging voltage  •  Capacitor discharge voltage  •  R/C for the charging voltage  •  Series circuit R/C  •  Parallel circuit R/C  •  Low pass-filter R/C  •  High pass-filter R/C  •  Integrator R/C  •  Differentiator R/C  •  Cutoff-frequency R,C  •  R and C for a given impedance  •