Schiefe Ebene berechnen

Rechner und Formeln zur Berechnung von einer schiefen Ebene

Schiefe Ebene Rechner

Kraftzerlegung auf schiefer Ebene

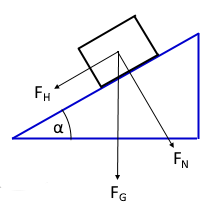
Berechnet die Kraftkomponenten auf einer schiefen Ebene: Gewichtskraft (FG), Hangabtrieb (FH) und Normalkraft (FN).

Schiefe Ebene
Kräfte auf der schiefen Ebene
N
Resultat
Gewichtskraft FG:
Hangabtrieb FH:
Normalkraft FN:

Beispielrechnung

Beispiel: Kiste auf schiefer Ebene
Aufgabe:

Eine Kiste mit 50 kg Masse liegt auf einer schiefen Ebene mit 30° Neigung. Berechnen Sie alle Kraftkomponenten (g = 9,81 m/s²).

Gegeben:
  • Masse m = 50 kg
  • Neigungswinkel α = 30°
  • g = 9,81 m/s²
  • FG = m × g = 50 × 9,81 = 490,5 N
Lösung:
Hangabtrieb (FH):
\[F_H = F_G \times \sin(\alpha)\] \[F_H = 490{,}5 \text{ N} \times \sin(30°)\] \[F_H = 490{,}5 \times 0{,}5 = 245{,}25 \text{ N}\]
Normalkraft (FN):
\[F_N = F_G \times \cos(\alpha)\] \[F_N = 490{,}5 \text{ N} \times \cos(30°)\] \[F_N = 490{,}5 \times 0{,}866 = 424{,}8 \text{ N}\]
Praktische Anwendungen
Straßenbau: Berechnung von Hangabtriebskräften für Fahrzeuge
Maschinenbau: Förderbänder, Rutschen, Rampen
Bauwesen: Dachkonstruktionen, Treppen, Böschungen
Wichtige Winkelwerte
  • 0°: sin = 0, cos = 1
  • 30°: sin = 0,5, cos = 0,866
  • 45°: sin = 0,707, cos = 0,707
  • 60°: sin = 0,866, cos = 0,5
  • 90°: sin = 1, cos = 0
  • Steigung 1:3 ≈ 18,4°

Formeln zur schiefen Ebene

Auf einer schiefen Ebene wird die Gewichtskraft in zwei Komponenten zerlegt: den Hangabtrieb (parallel zur Ebene) und die Normalkraft (senkrecht zur Ebene).

Hangabtrieb FH

Kraftkomponente parallel zur schiefen Ebene (Rutschkraft).

\[\displaystyle F_H = F_G \cdot \sin(\alpha)\]
Bewirkt die Bewegung entlang der Ebene.
Normalkraft FN

Kraftkomponente senkrecht zur schiefen Ebene.

\[\displaystyle F_N = F_G \cdot \cos(\alpha)\]
Drückt den Körper gegen die Ebene.
Gewichtskraft FG

Resultierende aus beiden Komponenten.

\[\displaystyle F_G = \sqrt{F_H^2 + F_N^2}\]
Oder: FG = m × g
Wichtige Hinweise
  • Bei α = 0° ist FH = 0 und FN = FG (horizontale Ebene)
  • Bei α = 90° ist FH = FG und FN = 0 (senkrechter Fall)
  • Der Hangabtrieb steigt mit zunehmendem Neigungswinkel
  • Die Normalkraft sinkt mit zunehmendem Neigungswinkel

Detaillierte Beschreibung der schiefen Ebene

Physikalische Grundlagen

Diese Funktion berechnet die Kräfte, die auf einer schiefen Ebene wirken. Die Gewichtskraft FG kann aufgeteilt werden in eine Komponente senkrecht zur schiefen Ebene (Normalkraftkomponente FN) und eine Komponente parallel zur schiefen Ebene (Hangabtrieb FH).

Bedienungshinweise

Geben Sie eine bekannte Kraft (FG, FH oder FN) und den Neigungswinkel ein. Der Rechner berechnet automatisch alle anderen Kraftkomponenten.

Anwendungsbereiche

Straßen- und Wegebau

Berechnung der Hangabtriebskräfte für Fahrzeuge auf geneigten Straßen. Wichtig für Bremswege und Traktion.

Maschinenbau

Förderbänder, Rutschen, Rampen, geneigte Förderanlagen. Dimensionierung von Antrieben und Bremssystemen.

Bauwesen

Dachkonstruktionen, Treppen, Böschungen, Rutschsicherheit. Statische Berechnungen für geneigte Bauteile.

Kraftzerlegung verstehen

Die Kraftzerlegung auf der schiefen Ebene ist ein fundamentales Konzept der Mechanik. Je steiler die Ebene, desto größer wird der Hangabtrieb:

Flache Ebene (15°)

FH = FG × sin(15°) ≈ 0,26 × FG
FN = FG × cos(15°) ≈ 0,97 × FG

Mittlere Neigung (45°)

FH = FG × sin(45°) ≈ 0,71 × FG
FN = FG × cos(45°) ≈ 0,71 × FG

Steile Ebene (75°)

FH = FG × sin(75°) ≈ 0,97 × FG
FN = FG × cos(75°) ≈ 0,26 × FG

Erkenntnis: Je steiler die Ebene, desto größer wird der Hangabtrieb und desto kleiner die Normalkraft!

Ist diese Seite hilfreich?            
Vielen Dank für Ihr Feedback!

Das tut uns leid

Wie können wir die Seite verbessern?


Weitere Physik Funktionen

Arbeit, Leistung und Zeit • Arbeit und Weg • Drehmoment • Druck, Kraft und Fläche • Gewichtskraft • Leistung, Kraft, Weg und Zeit • PS in kW umrechnen • PS in hp umrechnen • Schiefe Ebene • Wirkungsgrad • Zentrifugalkraft • Gravimetrische Energiedichte • Kinetische Energie • Volumetrische Energiedichte • Bahngeschwindigkeit • Beschleunigung nach Distanz • Beschleunigung nach Zeit • Geschwindigkeit, Weg und Zeit • Kreisbewegung • Winkelgeschwindigkeit • Fallgeschwindigkeit • Schalldruckpegel, Pacal und Dezibel • Schallgeschwindigkeit, Mach-Zahl • Schallgeschwindigkeit, Temperatur • Temperatur in der Atmosphäre • Getriebeübersetzung • Riemenlänge • Brechungswinkel