Vektor Subtraktion

Rechner und Formel zur Subtraktion von Vektoren (komponentenweise Differenz)

Vektor Subtraktion Rechner

Vektor Subtraktion

Berechnet die Differenz v₁ - v₂ zweier Vektoren durch komponentenweise Subtraktion: [x₁-x₂, y₁-y₂, z₁-z₂]

Voraussetzungen für Subtraktion

Vektoren können nur subtrahiert werden, wenn sie dieselbe Dimension und gleiche Orientierung (Spalten- oder Zeilenvektoren) haben.

Wählen Sie die Vektordimension
Minuend (v₁)
X-Komponente des ersten Vektors
Y-Komponente des ersten Vektors
Z-Komponente des ersten Vektors
W-Komponente des ersten Vektors
Subtrahend (v₂)
X-Komponente des zweiten Vektors
Y-Komponente des zweiten Vektors
Z-Komponente des zweiten Vektors
W-Komponente des zweiten Vektors
Subtraktionsergebnis
X:
Y:
Z:
W:
Differenzvektor:
Komponentenweise Subtraktion: v₁ - v₂ = [x₁-x₂, y₁-y₂, ...]

Subtraktion Info

Subtraktion Eigenschaften

Komponentenweise: Entsprechende Elemente werden subtrahiert

v₁ - v₂ Differenz Komponentenweise

Nicht kommutativ: v₁ - v₂ ≠ v₂ - v₁
Dimension: Gleiche Anzahl Komponenten erforderlich

Grafische Darstellung
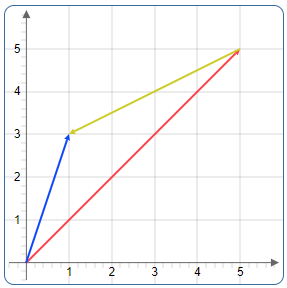
Vektorsubtraktion
Geometrische Interpretation der Vektorsubtraktion
Beispiele
[3,5] - [1,4] = [2,1]
[10,20,30] - [1,2,3] = [9,18,27]
[a,b,c] - [x,y,z] = [a-x,b-y,c-z]

Formeln für Vektor-Subtraktion

Allgemeine Formel
\[\vec{a} - \vec{b} = \begin{pmatrix} a_1 - b_1 \\ a_2 - b_2 \\ \vdots \\ a_n - b_n \end{pmatrix}\]

Komponentenweise Subtraktion

2D Subtraktion
\[\begin{pmatrix} a \\ b \end{pmatrix} - \begin{pmatrix} c \\ d \end{pmatrix} = \begin{pmatrix} a-c \\ b-d \end{pmatrix}\]

Zweidimensionale Vektoren

3D Subtraktion
\[\begin{pmatrix} a \\ b \\ c \end{pmatrix} - \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} a-x \\ b-y \\ c-z \end{pmatrix}\]

Dreidimensionale Vektoren

Geometrische Deutung
\[\vec{a} - \vec{b} = \vec{a} + (-\vec{b})\]

Subtraktion als Addition des Gegenvektors

Rechenbeispiele für Vektor-Subtraktion

Beispiel 1: 2D Subtraktion
[3, 5] - [1, 4]
\[\begin{pmatrix} 3 \\ 5 \end{pmatrix} - \begin{pmatrix} 1 \\ 4 \end{pmatrix} = \begin{pmatrix} 3-1 \\ 5-4 \end{pmatrix} = \begin{pmatrix} 2 \\ 1 \end{pmatrix}\]

Ergebnis: [2, 1]

Beispiel 2: 3D Subtraktion
[10, 20, 30] - [1, 2, 3]
\[\begin{pmatrix} 10 \\ 20 \\ 30 \end{pmatrix} - \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} = \begin{pmatrix} 10-1 \\ 20-2 \\ 30-3 \end{pmatrix} = \begin{pmatrix} 9 \\ 18 \\ 27 \end{pmatrix}\]

Ergebnis: [9, 18, 27]

Geometrische Interpretation
v₁ - v₂
Vektor von v₂ zu v₁
Nicht kommutativ
a - b ≠ b - a
Parallelogramm
Diagonalvektor

Die Subtraktion erzeugt den Vektor vom Subtrahend zum Minuend

Regeln und Einschränkungen
✓ Erlaubt

• Gleiche Dimension

• Gleiche Orientierung

• [a,b] - [c,d]

✗ Nicht erlaubt

• Verschiedene Dimensionen

• [a,b] - [c,d,e]

• Zeilen- vs Spaltenvektor

⚠ Beachten

• Nicht kommutativ

• Reihenfolge wichtig

• a - b ≠ b - a

Anwendungen der Vektor-Subtraktion

Vektor-Subtraktion ist fundamental für Bewegung, Differenzen und Richtungsberechnungen:

Navigation & Bewegung
  • Richtungsvektor zwischen zwei Punkten
  • Geschwindigkeitsdifferenzen berechnen
  • Relative Bewegung und Positionsänderung
  • GPS-Navigation und Pfadfindung
Computer Graphics
  • Objektbewegung und Transformation
  • Kollisionserkennung und -vermeidung
  • Kamera- und View-Transformationen
  • Animationen und Bewegungsinterpolation
Physik & Mechanik
  • Kraft- und Impulsdifferenzen
  • Relative Geschwindigkeiten berechnen
  • Schwerpunkt- und Massenmittelpunkt
  • Feldstärken und Potentiale
Datenanalyse
  • Differenzen zwischen Datensätzen
  • Trendanalyse und Änderungsvektoren
  • Feature-Differenzen in ML
  • Statistische Abweichungsanalyse

Vektor-Subtraktion: Differenzen im Vektorraum

Die Vektor-Subtraktion ist eine fundamentale Operation der linearen Algebra, die zwei Vektoren eine Differenz zuordnet. Diese komponentenweise Subtraktion folgt denselben Regeln wie die skalare Arithmetik, erweitert sie aber elegant in höhere Dimensionen. Geometrisch interpretiert erzeugt die Subtraktion v₁ - v₂ den Vektor, der vom Ende des zweiten zum Ende des ersten Vektors zeigt. Diese Operation ist zentral für Bewegungsberechnungen, Richtungsbestimmung und die Analyse von Vektor-Differenzen in Physik und Technik.

Zusammenfassung

Die Vektor-Subtraktion verbindet algebraische Einfachheit mit geometrischer Bedeutung. Die intuitive Regel - entsprechende Komponenten subtrahieren - erschließt fundamentale räumliche Beziehungen zwischen Punkten und Richtungen. Von der Navigation über Computergrafik bis zur Physik ermöglicht die Vektor-Subtraktion präzise Berechnungen relativer Positionen, Bewegungen und Veränderungen. Sie zeigt, wie elementare mathematische Operationen komplexe räumliche und zeitliche Zusammenhänge quantifizieren und computergestützt auswertbar machen können.

Ist diese Seite hilfreich?            
Vielen Dank für Ihr Feedback!

Das tut uns leid

Wie können wir die Seite verbessern?

Weitere Vektor Funktionen

Addition • Subtraktion • Multiplikation • Skalar Multiplikation • Division • Skalar Division • Skalarprodukt • Kreuzprodukt • Interpolation • Distanz • Distanz-Quadrat • Normierung • Spiegelung • Betrag • Betragsquadrat • Spatprodukt