Spatprodukt berechnen

Rechner und Formel zur Berechnung des Spatprodukts und Volumens dreier Vektoren

Spatprodukt Rechner

Spatprodukt (Scalar Triple Product)

Berechnet das Spatprodukt (a⃗ × b⃗) · c⃗ dreier Vektoren zur Volumenbestimmung des aufgespannten Parallelepipeds

Volumenberechnung mit drei 3D-Vektoren

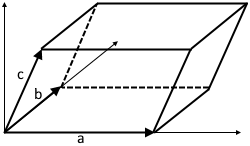
Das Spatprodukt berechnet das Volumen des Parallelepipeds, das von drei Vektoren im 3D-Raum aufgespannt wird.

Drei 3D-Vektoren eingeben
Vektor 1 (a⃗)
Vektor 2 (b⃗)
Vektor 3 (c⃗)
Spatprodukt-Ergebnis
Spatprodukt (a⃗ × b⃗) · c⃗:
Volumen des aufgespannten Parallelepipeds
Spatprodukt = (a⃗ × b⃗) · c⃗ = det(a⃗, b⃗, c⃗) = Volumen des Parallelepipeds

Spatprodukt Info

Spatprodukt Eigenschaften

Volumen: Misst das Volumen eines 3D-Parallelepipeds

3D Volumen Determinante Skalar

Zwei Methoden: (a⃗ × b⃗) · c⃗ oder det(a⃗, b⃗, c⃗)
Koplanar: Spatprodukt = 0 bei komplanaren Vektoren

Spatprodukt Visualisierung
Parallelepiped aufgespannt von drei Vektoren
Berechnungsmethoden
Methode 1: (a⃗ × b⃗) · c⃗
Methode 2: det(Matrix)

Formeln für das Spatprodukt

Kreuz- und Skalarprodukt
\[(\vec{a} \times \vec{b}) \cdot \vec{c}\]

Zuerst Kreuzprodukt, dann Skalarprodukt

Determinanten-Methode
\[\det\begin{pmatrix} a_1 & b_1 & c_1 \\ a_2 & b_2 & c_2 \\ a_3 & b_3 & c_3 \end{pmatrix}\]

3×3 Determinante berechnen

Kreuzprodukt-Formel
\[\vec{a} \times \vec{b} = \begin{pmatrix} a_2b_3 - a_3b_2 \\ a_3b_1 - a_1b_3 \\ a_1b_2 - a_2b_1 \end{pmatrix}\]

Für die erste Methode benötigt

Volumen-Interpretation
\[V = |(\vec{a} \times \vec{b}) \cdot \vec{c}|\]

Betrag für positives Volumen

Rechenbeispiele für das Spatprodukt

Beispiel: Methode 1 (Kreuz- & Skalarprodukt)
a⃗=[1,1,1], b⃗=[2,1,3], c⃗=[6,0,-2]
Schritt 1: Kreuzprodukt \[\vec{a} \times \vec{b} = \begin{pmatrix}2\\-1\\-1\end{pmatrix}\] Schritt 2: Skalarprodukt \[\begin{pmatrix}2\\-1\\-1\end{pmatrix} \cdot \begin{pmatrix}6\\0\\-2\end{pmatrix} = 12+0+2 = 14\]

Spatprodukt = 14

Beispiel: Methode 2 (Determinante)
Dieselben Vektoren als Matrix
\[\det\begin{pmatrix} 1 & 2 & 6 \\ 1 & 1 & 0 \\ 1 & 3 & -2 \end{pmatrix}\] \[= 1 \cdot 1 \cdot (-2) + 2 \cdot 0 \cdot 1 + 6 \cdot 1 \cdot 3\] \[- 6 \cdot 1 \cdot 1 - 1 \cdot 0 \cdot 3 - 2 \cdot 1 \cdot (-2) = 14\]

Spatprodukt = 14 (gleich!)

Geometrische Bedeutung
Spatprodukt > 0
Rechtssystem
Spatprodukt < 0
Linkssystem
Spatprodukt = 0
Koplanar (in einer Ebene)
|Spatprodukt|
Volumen des Parallelepipeds

Das Vorzeichen gibt die Orientierung an, der Betrag das Volumen

Schritt-für-Schritt Anleitung
Methode 1: Kreuz- & Skalarprodukt
  1. Kreuzprodukt a⃗ × b⃗ berechnen
  2. Skalarprodukt (a⃗ × b⃗) · c⃗ berechnen
  3. Ergebnis ist das Spatprodukt
Methode 2: Determinante
  1. Matrix aus drei Vektoren bilden
  2. 3×3 Determinante berechnen
  3. Determinante ist das Spatprodukt

Anwendungen des Spatprodukts

Das Spatprodukt ist fundamental für 3D-Geometrie und hat wichtige Anwendungen:

Geometrie & 3D-Modellierung
  • Volumenberechnung von Parallelepipeden
  • Orientierungstest (Links-/Rechtssystem)
  • Komplanarität von drei Vektoren prüfen
  • 3D-Objekterkennung und -klassifizierung
Computer Graphics
  • Backface Culling und Sichtbarkeit
  • 3D-Kollisionserkennung
  • Normale und Tangentialebenen
  • Ray Tracing und Lichtberechnung
Physik & Ingenieurswesen
  • Drehimpuls und Drehmomentberechnungen
  • Fluidmechanik: Wirbelstärke
  • Kristallographie: Einheitszellen
  • Elektromagnetismus: Feldberechnungen
Mathematik & Algebra
  • Lineare Unabhängigkeit prüfen
  • Basis-Vektoren und Koordinatensysteme
  • Determinanten von 3×3-Matrizen
  • Vektorraum-Dimensionalität

Spatprodukt: Volumen im dreidimensionalen Raum

Das Spatprodukt ist eine fundamentale Operation der 3D-Vektorrechnung, die drei Vektoren eine reelle Zahl zuordnet - das Volumen des von ihnen aufgespannten Parallelepipeds. Diese elegante Verknüpfung von Kreuz- und Skalarprodukt oder alternativ die Berechnung als 3×3-Determinante offenbart tiefe geometrische Zusammenhänge. Das Spatprodukt entscheidet über Komplanarität, bestimmt Orientierung und quantifiziert dreidimensionale Ausdehnung - unverzichtbar in Geometrie, Physik und Computer-Grafik.

Zusammenfassung

Das Spatprodukt vereint geometrische Anschauung mit algebraischer Präzision. Die zwei äquivalenten Berechnungswege - über Kreuz- und Skalarprodukt oder als Determinante - bieten sowohl konzeptionelle Klarheit als auch rechnerische Flexibilität. Von der Volumenbestimmung über Orientierungstests bis zur linearen Unabhängigkeitsprüfung erschließt das Spatprodukt fundamentale Eigenschaften des dreidimensionalen Raums. Es zeigt, wie elegant die Vektorrechnung komplexe räumliche Beziehungen in einer einzigen Zahl kodieren und messbar machen kann.

Ist diese Seite hilfreich?            
Vielen Dank für Ihr Feedback!

Das tut uns leid

Wie können wir die Seite verbessern?

Weitere Vektor Funktionen

Addition • Subtraktion • Multiplikation • Skalar Multiplikation • Division • Skalar Division • Skalarprodukt • Kreuzprodukt • Interpolation • Distanz • Distanz-Quadrat • Normierung • Spiegelung • Betrag • Betragsquadrat • Spatprodukt