Home

Interest Calculation

Description of the calculation of Interest with examples

Tutorial

Calculation of Interest


The interest calculation is an extension of the percentage calculation. Interest is a percent value of one underlying or principal.

Base of the percentage calculation is the formula \(\displaystyle \frac{Z}{K}=\frac{P}{100}\)


  • \(Z\) = Interest
  • \(K\) = Principal
  • \(P\) = Interest rate

The formula can be changed for the value you are looking for

Interest     \(\displaystyle Z=\frac{K · P}{100}\)


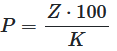
Principal    \(\displaystyle K=\frac{Z · 100}{P}\)


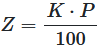
Interest rate   \(\displaystyle P=\frac{Z · 100}{K}\)


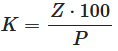
Calculate interest income


This example calculates the interest earned on investing \(3000\) for one year at a fixed rate of \(3\%\).

Given is the interest rate \(P = 3\) and the capital = \(3000\).

We are looking for the interest income \(Z\).

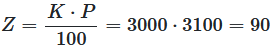
The interest income is calculated according to the formula \(\displaystyle Z=\frac{K·P}{100}={3000·3}{100}=90 \)



Calculate interest rate


This example calculates the interest rate, which is required to receive \(150$\) interest in one year, from a capital of \(3000$\).

The capital \(K = 300\) and the interest income \(Z = 150\) are known.

We are looking for the interest rate \(P\).

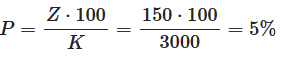
Calculated according to the formula \(\displaystyle P=\frac{Z·100}{K}=\frac{150·100}{3000}=5\%\)



Calculate starting capital


What amount must be invested in order to receive an interest income of \(200$\) at a rate of \(5%\)? This question should be solved in this task.

he interest rate of \(P = 5\%\) and the interest income \(Z = 200$\) are known

We are looking for starting capital \(K\).

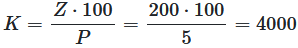
It is calculated according to the formula \(\displaystyle K=\frac{Z·100}{P}=\frac{200·100}{5}=4000\)



Calculate interest income daily


For example, suppose you want to invest \(5000$\) for \(2\) months at an annual interest rate of \(5\%\). For this, the interest must be calculated on a daily basis. The formula for calculating the interest income is extended accordingly by the number of \(Tage = t\). For each month, 30 days, so 360 days for 1 year are assume.

The capital \(K = 5000\), the interest rate \(P = 5\) and the number of days \(t = 60\) are known

We are looking for interest income \(Z\).

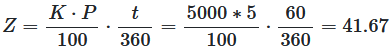
This is calculated \(\displaystyle Z=\frac{K·P}{100}·\frac{t}{360}=\frac{5000*5}{100}·\frac{60}{360}=41.67\)