Modulo Operation
Definition, properties, and applications of the remainder in Euclidean division
Introduction to Modulo
The modulo operation is a fundamental concept in mathematics and computer science that calculates the remainder of a division. It is denoted by the operator mod or % in most programming languages.
The modulo operation is closely related to the concept of Euclidean division, where any integer can be expressed as the product of a divisor and quotient, plus a remainder.
The modulo operation finds the remainder when one number (the dividend) is divided by another number (the divisor). For positive integers, this is straightforward; for negative integers, different definitions may apply depending on the context.
Definition of Modulo
In the Euclidean division of two integers, the modulo operation extracts the remainder from that division.
For integers \(a\) (dividend) and \(b\) (divisor, \(b \neq 0\)), the modulo operation \(\displaystyle a \bmod b\) returns the remainder \(r\) such that:
\(\displaystyle a = b \cdot q + r\) where \(\displaystyle 0 \leq r < |b|\)
Result of Modulo:
\(\displaystyle a \bmod b = r\)
In this formula:
- \(\displaystyle a\) is the dividend
- \(\displaystyle b\) is the divisor
- \(\displaystyle q\) is the quotient (integer division result)
- \(\displaystyle r\) is the remainder (the result of modulo operation)
Simple Examples of Modulo
- \(\displaystyle 17 \bmod 5 = 2\) (because \(\displaystyle 17 = 5 \cdot 3 + 2\))
- \(\displaystyle 20 \bmod 4 = 0\) (because \(\displaystyle 20 = 4 \cdot 5 + 0\))
- \(\displaystyle 13 \bmod 6 = 1\) (because \(\displaystyle 13 = 6 \cdot 2 + 1\))
- \(\displaystyle 7 \bmod 7 = 0\) (because \(\displaystyle 7 = 7 \cdot 1 + 0\))
- \(\displaystyle 3 \bmod 8 = 3\) (because \(\displaystyle 3 = 8 \cdot 0 + 3\))
Visual Example: 17 mod 5

Modulo with Different Signs
When dealing with negative numbers, the modulo operation can have different definitions depending on the mathematical convention or programming language used. Here are the main approaches:
Truncated Division (Programming Convention)
Most programming languages use truncated division, where the quotient is rounded toward zero.
| Division | Quotient | Remainder | Formula |
|---|---|---|---|
| \(\displaystyle 7 / 3\) | \(2\) | \(1\) | \(\displaystyle 7 = 3 \cdot 2 + 1\) |
| \(\displaystyle -7 / 3\) | \(-2\) | \(-1\) | \(\displaystyle -7 = 3 \cdot (-2) + (-1)\) |
| \(\displaystyle 7 / -3\) | \(-2\) | \(1\) | \(\displaystyle 7 = (-3) \cdot (-2) + 1\) |
| \(\displaystyle -7 / -3\) | \(2\) | \(-1\) | \(\displaystyle -7 = (-3) \cdot 2 + (-1)\) |
Visual Comparison of Different Sign Cases
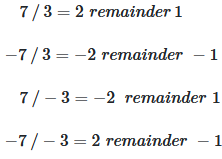
Different programming languages may handle modulo with negative numbers differently. Most languages (C, C++, Java) use truncated division, while others (Python, Ruby) use floored division.
Properties of Modulo
The modulo operation has several important mathematical properties that are useful in algebra and number theory.
Identity
\(\displaystyle a \bmod a = 0\)Any number modulo itself equals zero.
Modulo One
\(\displaystyle a \bmod 1 = 0\)Any integer modulo 1 equals zero.
Divisibility Test
\(\displaystyle a \equiv 0 \pmod{b} \iff b | a\)\(a\) is divisible by \(b\) if and only if \(a \bmod b = 0\).
Addition Rule
\(\displaystyle (a + b) \bmod n \) \(\displaystyle = ((a \bmod n) + (b \bmod n)) \)Modulo distributes over addition.
Multiplication Rule
\(\displaystyle (a \cdot b) \bmod n \) \(\displaystyle = ((a \bmod n) \cdot (b \bmod n)) \)Modulo distributes over multiplication.
Range of Result
\(\displaystyle 0 \leq (a \bmod b) < |b|\)The result is always less than the divisor (in absolute value).
Applications of Modulo
Mathematics and Number Theory
- Divisibility Testing: Checking if a number divides evenly into another
- Congruence: Determining if two numbers are equivalent modulo n
- Cyclic Patterns: Detecting repeating sequences with period n
- GCD and LCM: Euclidean algorithm uses modulo for computation
Computer Science and Programming
- Hashing: Creating hash codes and distributing data across buckets
- Cyclic Buffers: Managing circular queues and buffers
- Random Number Generation: Creating pseudo-random sequences
- Checking Even/Odd: \(\displaystyle n \bmod 2 = 0\) for even numbers
- Digit Extraction: Isolating specific digits from a number
Real-World Applications
- Clock Arithmetic: Time calculations (24-hour, 60-minute systems)
- Day of Week: Determining the day corresponding to any date
- Checksum Calculation: Error detection in data transmission
- Round-Robin Scheduling: Distributing tasks fairly among processors
Common Programming Examples
Even/Odd Check
Example: Determining if a Number is Even or Odd
\(\displaystyle n \bmod 2 = 0\) → Even
\(\displaystyle n \bmod 2 = 1\) → Odd
Example: \(\displaystyle 13 \bmod 2 = 1\) → 13 is odd ✓
Cycling Through Values
Example: Days of Week
If today is Friday (index 4), what day is it 10 days from now?
\(\displaystyle (4 + 10) \bmod 7 = 14 \bmod 7 = 0\) → Sunday (index 0) ✓
Last Digit Extraction
Example: Get the Last Digit
For number \(12345\): \(\displaystyle 12345 \bmod 10 = 5\) ✓
For number \(987\): \(\displaystyle 987 \bmod 10 = 7\) ✓
Common Mistakes to Avoid
WRONG: \(\displaystyle 17 \bmod 5\) gives the quotient ✗
RIGHT: \(\displaystyle 17 \bmod 5 = 2\) (the remainder) ✓
WRONG: \(\displaystyle 3 \bmod 8 = 3 + 8 = 11\) ✗
RIGHT: \(\displaystyle 3 \bmod 8 = 3\) (remainder must be less than divisor) ✓
WRONG: \(\displaystyle -7 \bmod 3 = -1\) is always wrong across all definitions ✗
RIGHT: Result depends on language: some give \(2\), others give \(-1\) ✓
|
|