Calculate Distance Between Two Points
Online calculator for calculating the distance between two points in the coordinate system
Distance Calculator
Coordinate Distance
Calculates the distance between two points A(x₁,y₁) and B(x₂,y₂) using the Pythagorean theorem.
Visualization
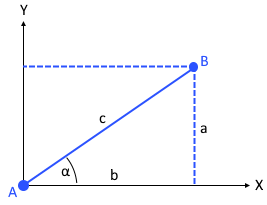
The graphic shows the geometric relationship between the two points A and B.
The resulting right triangle enables the application of the Pythagorean theorem.
|
|
How Does Distance Calculation Work?
The distance between two points is calculated using the distance formula:
- Input: Coordinates of points A(x₁,y₁) and B(x₂,y₂)
- Calculation: Application of the Pythagorean theorem
- Result: Direct distance between the points
- Additionally: Individual X and Y distances
- Angle: Inclination angle to the X-axis
- Order: Points A and B are interchangeable
The Pythagorean Theorem in Coordinate Geometry
The distance formula is based on the Pythagorean theorem:
Right Triangle
Basic formula of Pythagoras
Distance Formula
Applied to coordinates
Formulas and Calculations
Main Formula - Distance Between Two Points
The fundamental distance formula in coordinate geometry
Individual Coordinate Distances
Distances in X and Y directions (legs of the triangle)
Angle Calculation
Inclination angle of the connecting line to the X-axis
Alternative Angle Formulas
Angle calculation via sine and cosine
Example
Example Calculation
Calculation
The distance is 10 units
Individual Distances
- X-Distance: |8-0| = 8
- Y-Distance: |6-0| = 6
- Angle α: arctan(6/8) ≈ 36.87°
Applications
Navigation, cartography, computer graphics, robotics, GPS systems.
Construction of the Distance Formula
The distance formula between two points is based on the famous Pythagorean theorem. When we have two points A(x₁,y₁) and B(x₂,y₂) in a coordinate system, these together with a third point form a right triangle.
Geometric Derivation
In the graphic above, the two segments a and b form the legs of a right triangle. The segment c is the hypotenuse and corresponds to the desired distance between points A and B.
Coordinate Transformation
The values for the legs a and b result from the differences of the corresponding coordinates:
- Leg a (Y-direction): a = |y₂ - y₁|
- Leg b (X-direction): b = |x₂ - x₁|
Since we square the values, we can omit the absolute value signs, as (±n)² = n². This leads to the final distance formula:
|
|
|
|