Matrix Rotation
Rotate vectors in 2D and 3D using rotation matrices
Cartesian vs Polar Coordinates
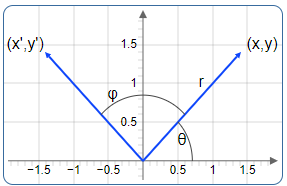
A point in the plane can be described in Cartesian coordinates as \((x, y)\). Alternatively, we can represent the same point using polar coordinates \((r, \theta)\), where \(r\) is the distance from the origin and \(\theta\) is the angle.
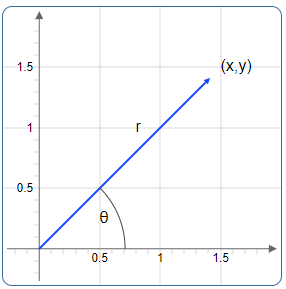
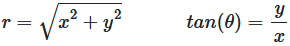
In the diagram above, \(r\) is the hypotenuse of a right-angled triangle.
\(x = r\cos(\theta)\) and \(y = r\sin(\theta)\)
2D Rotation and Rotation Matrix
The x-position can be calculated from the radius \(r\) and the angle \(\theta\) according to:
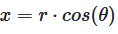
The y-position is calculated accordingly:
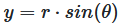
Rotate a Point by an Angle \(\varphi\)
If we rotate the point \((x, y)\) by the angle \(\varphi\), the new coordinates \((x', y')\) are:
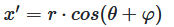
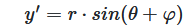
In matrix form, a rotation is written as:
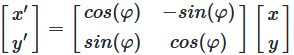
The 2D rotation matrix for an angle \(\varphi\) is:
Worked Example (\(\varphi = 30^\circ\))
The example below shows a rotation matrix for \(\varphi = 30^\circ\):
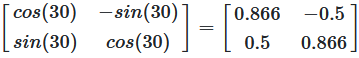
Rotate the vector (1, 0)
With this matrix, the position vector for the point \((1,0)\) becomes:
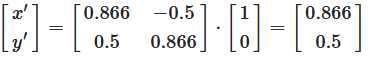
3D Rotation Matrices
In three-dimensional space, rotations are defined around a chosen axis. Below are counter-clockwise rotation matrices around the coordinate axes.
Rotation About the x-axis
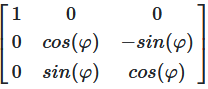
Rotation About the y-axis
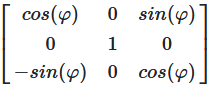
Rotation About the z-axis
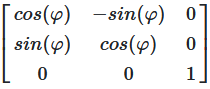
Rotation direction (clockwise vs counter-clockwise) depends on the chosen coordinate system and the sign convention for \(\varphi\). This page uses counter-clockwise rotations.
Key Points to Remember
2D Rotation
\(\mathbf{v}' = R(\varphi)\mathbf{v}\) with sine/cosine matrixPolar Link
\(x=r\cos(\theta)\), \(y=r\sin(\theta)\) explain the rotation formulas3D Rotations
Use axis-specific rotation matrices around x, y, zMatrices Calculation
Matrices Addition
Matrices Subtraction
Matrices Multiplication
Matrices Inverse Cramer method
Matrices Inverse Gauss-Jordan
Matrices and Simultaneous Equations
Matrices and Determinants
Row Operations of Matrices
Matrices and Geometry, Reflection
Matrices and Geometry, Plane Rotation
|
|