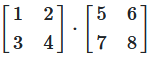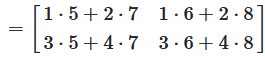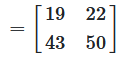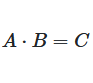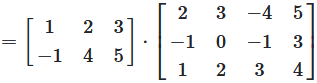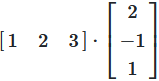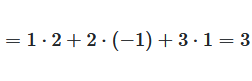Matrices Multiplication

We can calculate with matrices, just as we do arithmetic with numbers. We can matrices calculate if we follow the rules for their arithmetic.

Because of this similarity, it is useful to distinguish between numbers and matrices in the way that we write symbols of numbers by lower case letters \((a, b, x, y)\) and matrices by upper case (capital) letters such as\((A, B, X, Y)\).

Rules of matrix multiplication

There is a special rule for matrices multiplying, constructed in a way that is designed so that we can use it to represent simultaneous equations using matrices.

Multiplication of matrices is only allowed if the number of columns of the left matrix is the same as the number of rows of the right matrix.

The following matrices can be multiplied

The following matrices can not be multiplied

...because the number of columns in the left matrix does not match the number of rows in the right matrix.

The product of a matrix is calculated by taking the product sums of the pairs of row vectors of the first matrix and the column vectors of the second matrix

Example

\(\begin{bmatrix} a & b \\ c & d \end{bmatrix} \cdot \begin{bmatrix} i & j \\ k & l \end{bmatrix} = \begin{bmatrix} a\cdot i + b\cdot k & a\cdot j+ b\cdot l \\ c \cdot i + d \cdot k & c\cdot j + d\cdot l \end{bmatrix} \)

Example without a solution

The first element of the product \(C\), is the sum of the products of each element of the first row of \(A\), and the corresponding element of the first column of \(B\)

Matrix multiplication online calculator →