Matrixrotation und Drehungen
Rotation von Punkten und Vektoren in 2D und 3D mit Transformationsmatrizen
Rotation ist eine der wichtigsten geometrischen Transformationen. Mit Hilfe von Matrizen können wir Punkte und Vektoren um einen beliebigen Winkel drehen — in 2D um den Ursprung oder in 3D um eine Achse.
Dies wird besonders in der Computergrafik, Animation, Robotik und Physik-Simulation verwendet, um Objekte im Raum zu drehen und zu transformieren.
Polarkoordinaten
Die Grundlage für Rotationen bilden Polarkoordinaten. Ein Punkt kann entweder durch kartesische Koordinaten (x, y) oder durch Polarkoordinaten (r, θ) beschrieben werden.
- Kartesische Koordinaten: (x, y) - Abstände von den Achsen
- Polarkoordinaten: (r, θ) - Radius und Winkel vom Ursprung
- r = Radius: Die Entfernung vom Ursprung
- θ = Winkel: Der Winkel gemessen von der positiven X-Achse (gegen Uhrzeigersinn)
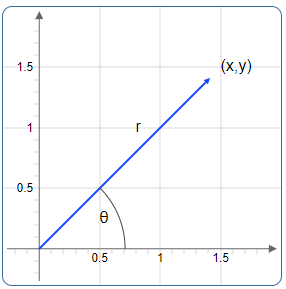
Abbildung 1: Punkt in kartesischen und Polarkoordinaten
Umwandlung zwischen Koordinatensystemen
r = √(x² + y²)
tan(θ) = y/x
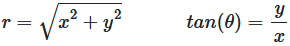
Abbildung 2: Formeln für Koordinaten-Umwandlung
Der Radius r ist die Hypotenuse des rechtwinkligen Dreiecks, wobei x und y die beiden Katheten sind.
Rückwandlung: Polar zu Kartesisch
Wenn wir den Radius r und den Winkel θ kennen, können wir die kartesischen Koordinaten berechnen.
Berechnung der X-Koordinate
x = r · cos(θ)
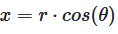
Abbildung 3: Berechnung der X-Koordinate aus Polarkoordinaten
Berechnung der Y-Koordinate
y = r · sin(θ)
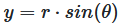
Abbildung 4: Berechnung der Y-Koordinate aus Polarkoordinaten
Rotation in 2D
Wenn wir einen Punkt (x, y) um einen Winkel φ drehen, bleibt der Radius r erhalten, aber der Winkel wird um φ erhöht.
Die Rotationsidee
Ein Punkt P mit Polarkoordinaten (r, θ) wird gedreht um φ zu:
x' = r · cos(θ + φ)
y' = r · sin(θ + φ)
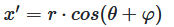
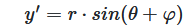
Abbildung 5-6: Formeln für die rotierten Koordinaten
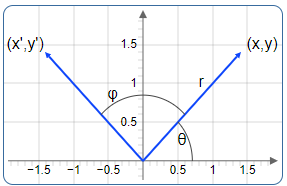
Abbildung 7: Visualisierung einer Drehung um Winkel φ
Die Rotationsmatrix für 2D
Die Rotation kann elegant in Matrixform geschrieben werden:
R(φ) = [cos(φ) -sin(φ)]
[sin(φ) cos(φ)]
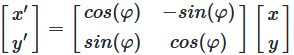
Abbildung 8: Die 2D Rotationsmatrix in allgemeiner Form
Praktisches Beispiel: Rotation um 30°
Rotation um φ = 30°
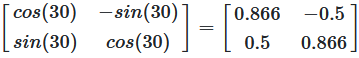
Abbildung 9: Rotationsmatrix für 30°
Beispiel: Punkt (1, 0) um 30° drehen
Anwendung der Rotationsmatrix
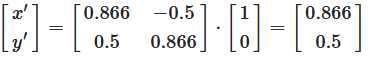
Abbildung 10: Berechnung des rotierten Punktes
Rotation in 3D
In drei Dimensionen können wir um eine der drei Koordinatenachsen drehen. Die Rotation erfolgt immer gegen den Uhrzeigersinn, wenn man von der positiven Achse blickt.
Rotation um die X-Achse
Bei Rotation um die X-Achse bleibt die X-Koordinate unverändert, während Y und Z rotieren:
R_x(φ) = [1 0 0 ]
[0 cos(φ) -sin(φ)]
[0 sin(φ) cos(φ)]
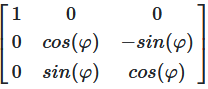
Abbildung 11: Rotationsmatrix für Drehung um die X-Achse
Rotation um die Y-Achse
Bei Rotation um die Y-Achse bleibt die Y-Koordinate unverändert, während X und Z rotieren:
R_y(φ) = [ cos(φ) 0 sin(φ)]
[ 0 1 0 ]
[-sin(φ) 0 cos(φ)]
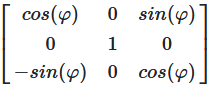
Abbildung 12: Rotationsmatrix für Drehung um die Y-Achse
Rotation um die Z-Achse
Bei Rotation um die Z-Achse bleibt die Z-Koordinate unverändert, während X und Y rotieren (ähnlich wie die 2D-Rotation):
R_z(φ) = [cos(φ) -sin(φ) 0]
[sin(φ) cos(φ) 0]
[ 0 0 1]
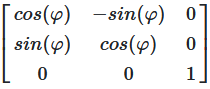
Abbildung 13: Rotationsmatrix für Drehung um die Z-Achse
Überblick: Rotationsmatrizen
| Achse | Koeffizient (cos φ) | Koeffizient (sin φ) | Feste Koordinate |
|---|---|---|---|
| X-Achse | In Y-Z Ebene | In Y-Z Ebene | X bleibt gleich |
| Y-Achse | In X-Z Ebene | In X-Z Ebene (negative Anordnung) | Y bleibt gleich |
| Z-Achse | In X-Y Ebene | In X-Y Ebene | Z bleibt gleich |
Wichtige Eigenschaften von Rotationen
Radius bleibt erhalten
Der Abstand vom Ursprung ändert sich nicht bei einer Rotation
Orthogonale Matrix
Rotationsmatrizen sind orthogonal: R · Rᵀ = I
Determinante = 1
Die Determinante ist immer 1 (keine Skalierung)
Kombinierbar
Rotationen können durch Matrizenmultiplikation kombiniert werden
Praktische Anwendungen
- Computergrafik: 3D-Rendering und Animation von Objekten
- Robotik: Steuerung von Roboterarmen und deren Ausrichtung
- Animation: Bewegungen und Drehungen von Charakteren
- Physik-Simulation: Rotation von Objekten unter Einfluss von Kräften
- Luftfahrt: Flugdynamik und Steuerung von Flugzeugen
- Bildverarbeitung: Drehung und Ausrichtung von Bildern
Tipps und häufige Fehler
- Winkelkonvention: Positive Winkel sind gegen den Uhrzeigersinn (mathematische Konvention)
- Radiant vs. Grad: Achte darauf, ob sin/cos in Radiant oder Grad arbeitet
- Reihenfolge wichtig: Bei mehreren Rotationen ist die Reihenfolge entscheidend
- Radius-Eigenschaft: Nutze die Tatsache, dass der Radius erhalten bleibt, um zu testen
- Visualisieren: Zeichne die Rotation, um sie zu verstehen
- FALSCH: Vorzeichen von sin in der falschen Position | RICHTIG: Beachte das Minus vor sin(φ)
- FALSCH: Gradmaß statt Radiant | RICHTIG: Konvertiere zu Radiant wenn nötig
- FALSCH: Rotation um falsche Achse | RICHTIG: Überprüfe, welche Koordinate fest bleibt
- FALSCH: Radius ändert sich | RICHTIG: Radius sollte immer gleich bleiben
Online-Rechner
Teste die Rotationen mit unserem interaktiven Online-Rechner:
|
|