Matrix Reflection and Shear

Use matrices to perform geometric transformations of vectors in 2D and 3D

Geometric Transformations with Matrices

Many geometric operations (reflection, shear, rotation, scaling) can be achieved by multiplying a position vector by a suitable matrix. In this tutorial we focus on reflection and shear.

Main Idea:

A transformation maps an input vector \(\mathbf{v}\) to an output vector \(\mathbf{v}'\) using \(\mathbf{v}' = A\mathbf{v}\).

Matrix Reflection (2D)

Consider a point \(P\) with coordinates \((x, y)\) in a two-dimensional space. We represent it as a vector:

\(\displaystyle \mathbf{v} = \begin{bmatrix}x \\ y\end{bmatrix}\)
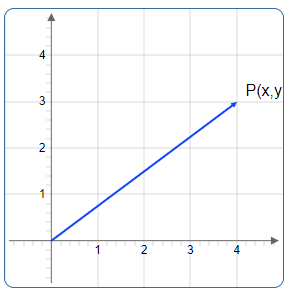
2D vector visualization

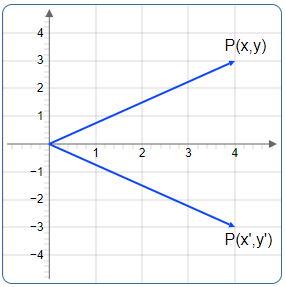
Reflection Across the X-Axis

The matrix below reflects a vector across the x-axis (the y-coordinate flips sign):

\(\displaystyle R_x = \begin{bmatrix}1 & 0 \\ 0 & -1\end{bmatrix}\)

Applying it to \(\mathbf{v}\) gives:

\(\displaystyle \mathbf{v}' = \begin{bmatrix}x' \\ y'\end{bmatrix} = R_x\mathbf{v} = \begin{bmatrix}1 & 0 \\ 0 & -1\end{bmatrix}\begin{bmatrix}x \\ y\end{bmatrix} = \begin{bmatrix}x \\ -y\end{bmatrix}\)
Reflection across x-axis

Matrix Reflection (3D)

In three dimensions, a reflection that flips the \(y\)-coordinate can be achieved by putting \(-1\) on the corresponding diagonal element of the identity matrix:

\(\displaystyle \begin{bmatrix}x' \\ y' \\ z'\end{bmatrix} = \begin{bmatrix}1 & 0 & 0 \\ 0 & -1 & 0 \\ 0 & 0 & 1\end{bmatrix}\begin{bmatrix}x \\ y \\ z\end{bmatrix} = \begin{bmatrix}x \\ -y \\ z\end{bmatrix}\)
General Rule:

To reflect in the \(X\)-, \(Y\)- or \(Z\)-plane, place a negative sign on the corresponding diagonal element of the identity matrix.

Matrix Shear (2D)

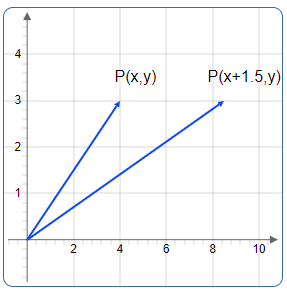
A shear transformation is produced by inserting a non-zero element outside the diagonal of the identity matrix. This shifts one coordinate proportionally to the other.

Shear Matrix Example

\(\displaystyle S = \begin{bmatrix}1 & 1.5 \\ 0 & 1\end{bmatrix}\)
Apply Shear to a Vector

Input: \(\mathbf{v} = \begin{bmatrix}4 \\ 3\end{bmatrix}\)

\(\displaystyle \begin{bmatrix}x' \\ y'\end{bmatrix} = S\mathbf{v} = \begin{bmatrix}1 & 1.5 \\ 0 & 1\end{bmatrix}\begin{bmatrix}4 \\ 3\end{bmatrix} = \begin{bmatrix}8.5 \\ 3\end{bmatrix}\)
Shear visualization

Key Points to Remember

Reflection
Reflection flips the sign of one coordinate via a negative diagonal entry
Shear
Shear uses a non-zero off-diagonal element to shift one coordinate proportionally
Matrix Multiplication
Transformations are applied as \(\mathbf{v}' = A\mathbf{v}\)














Is this page helpful?            
Thank you for your feedback!

Sorry about that

How can we improve it?