Matrizenspiegelung und Transformationen
Geometrische Transformationen mit Matrizen
Geometrische Transformationen wie Drehungen, Spiegelungen und Verschiebungen können elegantly mit Matrizen dargestellt werden. Dies ist ein mächtiges Werkzeug in der Computergrafik, Animation und Geometrie.
Indem wir einen Positionsvektor mit einer speziellen Transformationsmatrix multiplizieren, können wir den Punkt im Raum transformieren — drehen, spiegeln oder verzerren.
Vektoren und Koordinaten
Bevor wir mit Transformationen arbeiten, müssen wir verstehen, wie Punkte als Vektoren dargestellt werden.
2D-Punkt P mit Koordinaten (x, y)
Ein Punkt P im zweidimensionalen Raum mit Koordinaten (x, y) wird als Spaltenvektor dargestellt:
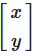
Abbildung 1: 2D-Punkt als Spaltenvektor
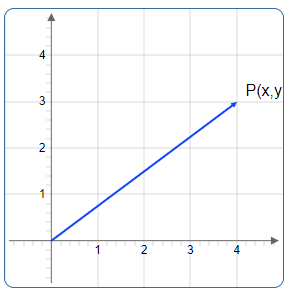
Abbildung 2: Visualisierung des Punktes im 2D-Koordinatensystem
3D-Punkt mit Koordinaten (x, y, z)
Im dreidimensionalen Raum wird ein Punkt analog als Spaltenvektor mit drei Komponenten dargestellt:
P = [x, y, z]ᵀ
Spiegelung in 2D
Spiegelungen sind eine wichtige geometrische Transformation. Es gibt verschiedene Arten von Spiegelungen.
Spiegelung über die X-Achse
Bei einer Spiegelung über die X-Achse bleibt die x-Koordinate gleich, aber die y-Koordinate wechselt das Vorzeichen.
S_x = [1 0]
[0 -1]
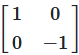
Abbildung 3: Spiegelungsmatrix für X-Achsen-Spiegelung
Anwendung der Spiegelung
Punkt über X-Achse spiegeln
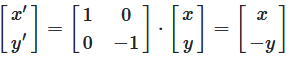
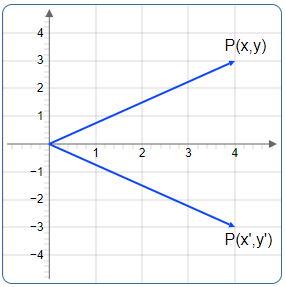
Abbildung 4-5: Spiegelung eines Punktes über die X-Achse
Spiegelung über die Y-Achse
S_y = [-1 0]
[0 1]
Die y-Koordinate bleibt gleich, die x-Koordinate wechselt das Vorzeichen.
Spiegelung über die Diagonale (y = x)
S_diag = [0 1]
[1 0]
Tauscht x und y Koordinaten: (x, y) → (y, x)
Spiegelung in 3D
In drei Dimensionen gibt es mehr Möglichkeiten für Spiegelungen — über die XY-, XZ- oder YZ-Ebenen.
Spiegelung über die XY-Ebene (Z-Vorzeichen wechseln)
S_xy = [1 0 0]
[0 1 0]
[0 0 -1]
Spiegelung über die YZ-Ebene (X-Vorzeichen wechseln)
S_yz = [-1 0 0]
[0 1 0]
[0 0 1]
Spiegelung über die XZ-Ebene (Y-Vorzeichen wechseln)
S_xz = [1 0 0]
[0 -1 0]
[0 0 1]
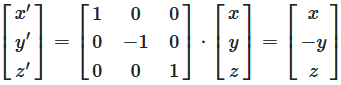
Abbildung 6: 3D-Spiegelung über die YZ-Ebene
Scherung (Shearing)
Eine Scherverzerrung ist eine Transformation, bei der Punkte parallel zu einer Achse verschoben werden. Dies wird erreicht, indem Elemente außerhalb der Diagonalen in die Identitätsmatrix eingefügt werden.
Scherung in X-Richtung
Sh_x = [1 k]
[0 1]
wobei k der Scherungsparameter ist (bestimmt die Stärke der Verzerrung)
Praktisches Beispiel: Scherung mit k = 1.5
Punkt unter Scherung transformieren
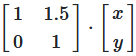
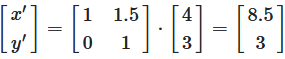
Abbildung 7-8: Scherungstransformation
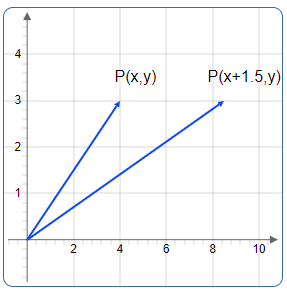
Abbildung 9: Visualisierung der Scherungstransformation
Scherung in Y-Richtung
Sh_y = [1 0]
[k 1]
Überblick: Transformationsmatrizen
| Transformation | 2D-Matrix | Effekt |
|---|---|---|
| Spiegelung X-Achse | [1 0; 0 -1] | (x, y) → (x, -y) |
| Spiegelung Y-Achse | [-1 0; 0 1] | (x, y) → (-x, y) |
| Spiegelung y=x | [0 1; 1 0] | (x, y) → (y, x) |
| Scherung X | [1 k; 0 1] | (x, y) → (x+ky, y) |
| Scherung Y | [1 0; k 1] | (x, y) → (x, kx+y) |
Kombination von Transformationen
Eine wichtige Eigenschaft ist, dass Transformationen kombiniert werden können durch Matrizenmultiplikation.
P'' = T₂ · T₁ · P
Zwei Transformationen T₁ und T₂ können kombiniert werden, indem man die Matrizen multipliziert. Achtung: Die Reihenfolge ist wichtig (nicht kommutativ)!
Beispiel: Spiegelung dann Scherung
Praktische Anwendungen
- Computergrafik: Transformation von 3D-Modellen und Rendering
- Animation: Bewegung und Deformation von Charakteren
- CAD/CAM: Design und Fertigung von Objekten
- Bildverarbeitung: Geometrische Transformationen von Bildern
- Robotik: Bewegungsplanung und Koordinatentransformationen
- Physik-Simulation: Deformation von Objekten
Tipps und häufige Fehler
- Vorzeichen: Bei Spiegelungen ändert sich das Vorzeichen der entsprechenden Koordinate
- Identitätsmatrix: Nicht-Diagonalelemente führen zu Scherung/Verzerrung
- Reihenfolge: Bei kombinierten Transformationen ist die Reihenfolge der Multiplikation wichtig
- Visualisieren: Zeichne die Transformation, um das Ergebnis zu überprüfen
- Test-Punkte: Verwende einfache Punkte wie (1,0), (0,1) um die Wirkung zu verstehen
- FALSCH: Multiplikationsreihenfolge: P · T statt T · P | RICHTIG: T · P (Matrizenmultiplikation nicht kommutativ)
- FALSCH: Spiegelung mit falschen Vorzeichen | RICHTIG: Nur die entsprechende Koordinate negieren
- FALSCH: Transformationen in falscher Reihenfolge kombinieren | RICHTIG: Beachte die Anwendungsreihenfolge
- FALSCH: 2D-Matrix für 3D-Transformationen verwenden | RICHTIG: Dimensionen müssen passen
|
|