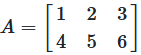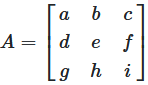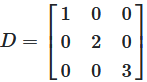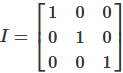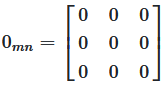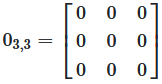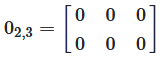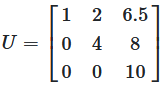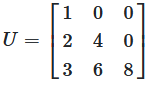Matrix Definition
Description of matrices definition with examples
A matrix (plural matrices) is a group of mathematical objects in a rectangular arrangement, like the figure below. With these matrices can be calculated in certain ways. For example, by adding or multiplying matrices. This article gives an overview of the different types of matrices.
The dimensions of the matrix are called \(p\) and \(q\).
A \(p · q\) - Matrix has \(p\) rows and \(q\) columns.
The position of an element is indicated by a double index. In the term \(a_{ij}\), \(i\) denotes the index of the line and \(j\) the index of the column.
Square Matrix
A square matrix is called a matrices that split an equal number and have rows.
Matrices Calculation
Matrices Addition
Matrices Subtraction
Matrices Multiplication
Matrices Inverse Cramer method
Matrices Inverse Gauss-Jordan
Matrices and Simultaneous Equations
Matrices and Determinants
Row Operations of Matrices
Matrices and Geometry, Reflection
Matrices and Geometry, Plane Rotation
Diagonal Matrix
A diagonal matrix is square and all non-diagonal elements are zero.
Identity Matrix or Unit Matrix
An identity matrix or unit matrix is a quadratic matrix whose main diagonal is filled with ones. All other elements are null.
Zero Matrix or Null Matrix
A zero matrix or null matrix is a matrix where all elements are zero. Written as \(0_{mn}\).
Upper Triangular Matrix
An upper triangular matrix has all elements below the diagonal element equal to zero.
Lower Triangular Matrix
A lower triangular matrix has all elements above the diagonal element equal to zero.
Matrices of one column or row are called vectors. Matrices with one column are column vectors. Likewise, matrices with one row are row vectors.
Matrices or vectors may be transpose. That means that the 1st row becomes the 1st column, the 2nd row the 2nd column, etc. The symbol to indicate a transpose is usually a capital superscript \(T\).
|
|