Matrizen Definition
Grundlagen, Typen und Notation von Matrizen
Eine Matrix (Plural: Matrizen) ist ein fundamentales mathematisches Objekt, das aus Zahlen in einer rechteckigen Anordnung besteht. Matrizen werden zur Darstellung von Daten, zur Lösung von Gleichungssystemen und in vielen praktischen Anwendungen verwendet.
Mit Matrizen können mathematische Operationen durchgeführt werden: Addition, Subtraktion, Multiplikation und viele mehr. Sie sind zentral für die lineare Algebra und haben breite Anwendungen in Naturwissenschaft, Technik und Informatik.
Grundbegriffe und Notation
Eine Matrix besteht aus Elementen, die in Zeilen und Spalten angeordnet sind.
- p × q Matrix: Hat p Zeilen und q Spalten
- Dimensionen: Werden als (p, q) oder p × q geschrieben
- Element a_ij: Das Element in Zeile i und Spalte j
- Matrixname: Matrizen werden mit Großbuchstaben bezeichnet (A, B, C, ...)
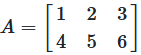
Abbildung 1: Eine 2 × 3 Matrix mit Element a_ij
Beispiel: Beschreibung einer Matrix
- Matrix A: Eine 2 × 3 Matrix mit 2 Zeilen und 3 Spalten
- Element a₁₁ = 1: Erste Zeile, erste Spalte
- Element a₂₃ = 6: Zweite Zeile, dritte Spalte
- Gesamte Elemente: 6 Elemente total (2 × 3 = 6)
Wichtige Matrixtypen
1. Quadratische Matrix
Eine quadratische Matrix hat die gleiche Anzahl von Zeilen und Spalten (n × n).
- Anzahl Zeilen = Anzahl Spalten
- Die Hauptdiagonale geht von links oben nach rechts unten
- Wichtig für Determinanten und Invertierbarkeit

Abbildung 2: Eine 3 × 3 quadratische Matrix
2. Diagonalmatrix
Eine Diagonalmatrix ist eine quadratische Matrix, bei der nur die Diagonalelemente ungleich Null sind.
- Alle Nicht-Diagonalelemente sind 0
- Nur a_ii kann ungleich Null sein
- Einfach zu verarbeiten bei Berechnungen
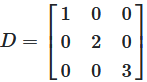
Abbildung 3: Eine Diagonalmatrix mit Elementen 1, 2, 3
3. Einheitsmatrix (Identitätsmatrix)
Die Einheitsmatrix (oder Identitätsmatrix) ist eine Diagonalmatrix, bei der alle Diagonalelemente gleich 1 sind.
- Symbol: I oder I_n (für n × n Einheitsmatrix)
- Alle Diagonalelemente sind 1
- Alle anderen Elemente sind 0
- Neutrale Element der Matrizenmultiplikation: A · I = A
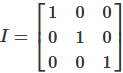
Abbildung 4: Die 3 × 3 Einheitsmatrix
4. Nullmatrix
Eine Nullmatrix ist eine Matrix, bei der alle Elemente gleich Null sind.
- Symbol: 0 oder 0_{m,n} (für m × n Nullmatrix)
- Alle Elemente sind 0
- Kann beliebig groß sein (verschiedene Dimensionen möglich)
- Neutrales Element der Matrizenaddition: A + 0 = A
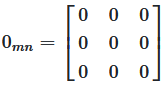
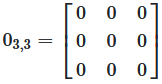
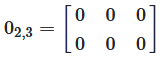
Abbildung 5: Verschiedene Nullmatrizen (3×3, 3×3, 2×3)
5. Obere Dreiecksmatrix
Bei einer oberen Dreiecksmatrix sind alle Elemente unterhalb der Hauptdiagonale gleich Null.
- a_ij = 0 für alle i > j
- Nicht-Null-Elemente nur auf und oberhalb der Diagonale
- Wichtig bei der Gaußschen Elimination
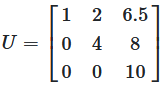
Abbildung 6: Eine obere Dreiecksmatrix
6. Untere Dreiecksmatrix
Bei einer unteren Dreiecksmatrix sind alle Elemente oberhalb der Hauptdiagonale gleich Null.
- a_ij = 0 für alle i < j
- Nicht-Null-Elemente nur auf und unterhalb der Diagonale
- Auch wichtig bei Zerlegungsverfahren
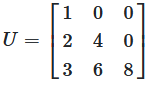
Abbildung 7: Eine untere Dreiecksmatrix
Vektoren als spezielle Matrizen
Vektoren sind Matrizen mit nur einer Zeile oder einer Spalte.
Spaltenvektor
Eine m × 1 Matrix
Eine Spalte, mehrere Zeilen
Zeilenvektor
Eine 1 × n Matrix
Eine Zeile, mehrere Spalten
Beispiele von Vektoren
- Spaltenvektor: v = [1, 2, 3]^T (eine Spalte, drei Zeilen)
- Zeilenvektor: w = [4, 5, 6] (eine Zeile, drei Spalten)
Transponierung einer Matrix
Die Transponierung einer Matrix ist eine Umwandlung, bei der Zeilen und Spalten vertauscht werden.
- Symbol: A^T oder A' (A-Transponiert)
- Operation: Die 1. Zeile wird die 1. Spalte, die 2. Zeile wird die 2. Spalte, etc.
- Formal: (A^T)_ij = A_ji
- Dimension: Wenn A eine m × n Matrix ist, ist A^T eine n × m Matrix
Beispiel einer Transponierung
Original Matrix A (2 × 3):
A = [1, 2, 3]
[4, 5, 6]
Transponierte A^T (3 × 2):
A^T = [1, 4]
[2, 5]
[3, 6]
Zeile 1 von A [1, 2, 3] wird Spalte 1 von A^T
Eigenschaften der Transponierung
- (A^T)^T = A: Die Transponierte der Transponierten ist die Originalmatrix
- (A + B)^T = A^T + B^T: Additiv
- (A · B)^T = B^T · A^T: Bei Multiplikation wird die Reihenfolge umgekehrt
- (c·A)^T = c·A^T: Skalarmultiplikation kommutativ mit Transponierung
Übersicht der Matrixtypen
| Matrixtyp | Dimension | Eigenschaft | Symbol |
|---|---|---|---|
| Quadratisch | n × n | Zeilen = Spalten | A |
| Diagonal | n × n | Nur Diagonale ≠ 0 | D |
| Einheit | n × n | Diagonale = 1, Rest = 0 | I, I_n |
| Null | m × n | Alle Elemente = 0 | 0, 0_{m,n} |
| Obere Dreieck | n × n | Unter Diagonale = 0 | U |
| Untere Dreieck | n × n | Über Diagonale = 0 | L |
| Spaltenvektor | m × 1 | Eine Spalte | v |
| Zeilenvektor | 1 × n | Eine Zeile | w |
Praktische Anwendungen
Lineare Gleichungssysteme
- Koeffizientenmatrix: Darstellung von Gleichungssystemen
- Lösungsmethoden: Gaußsches Eliminationsverfahren nutzt Dreiecksmatrizen
Computergrafik
- Transformationen: Rotationen, Skalierungen, Verschiebungen als Matrizen
- 3D-Rendering: Projektionsmatrizen für Perspektive
Naturwissenschaften und Technik
- Physik: Spannungstensor, Trägheitstensor
- Elektronik: Schaltungsanalyse mit Admittanzmatrizen
- Maschinenbau: Steifigkeitsmatrizen
Datenwissenschaft und Machine Learning
- Datenrepräsentation: Jede Zeile ein Datensatz, jede Spalte ein Merkmal
- Neuronale Netze: Gewichtsmatrizen in Layern
Wichtige Hinweise und Tipps
- Indizierung: Die Notation a_ij bedeutet immer Zeile i, Spalte j
- Reihenfolge: Zeilen werden zuerst genannt, dann Spalten (m × n)
- Diagonale: Nur bei quadratischen Matrizen definiert
- Transponierung: Spalten werden zu Zeilen und umgekehrt
- Identität: I · A = A = A · I (nur wenn Dimensionen passen)
|
|