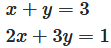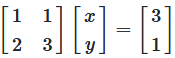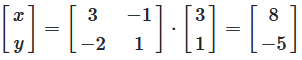Matrices and Simultaneous Equations
Description of matrices and simultaneous equations
The matrix multiplication can be used to calculate simultaneous equations.
The equations
is conformed to the following matrix expression by applying the multiplication rule
The way that multiplying matrices allows a whole set of linear equations to be written as a single equation, containing matrices instead of numbers.
If the symbols in this equation are numbers, it is easily solve it by division. Even though we have symbols, we can avoid using division, when we multiply with reciprocal value. Instead of dividing by \(x\), we can just as well multiply by \(x^{-1}\).
The inverse of a matrix is not easy to calculate, and you can only find an inverse if the matrix is a square matrix and even then, not always.
In this case above the inverse of
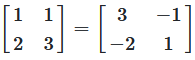
Now you can use the inverse above to calculate the values of \(x\) and \(y\).
The result is \(x = 8\) and \(y = -5\)
Matrices Calculation
Matrices Addition
Matrices Subtraction
Matrices Multiplication
Matrices Inverse Cramer method
Matrices Inverse Gauss-Jordan
Matrices and Simultaneous Equations
Matrices and Determinants
Row Operations of Matrices
Matrices and Geometry, Reflection
Matrices and Geometry, Plane Rotation
|
|