Matrizen und Simultane Gleichungen
Lösung linearer Gleichungssysteme mit Matrizen
Eines der wichtigsten praktischen Anwendungen von Matrizen ist die Lösung von simultanen (linearen) Gleichungssystemen. Mit Matrixalgebra können komplexe Gleichungssysteme elegant und systematisch gelöst werden.
Anstatt jede Gleichung einzeln zu manipulieren, können wir das gesamte System als eine einzige Matrixgleichung schreiben und dann mit Matrizenmultiplikation und Inversion lösen.
Von Gleichungen zu Matrizen
Jedes System linearer Gleichungen kann in eine Matrixgleichung umgewandelt werden.
Schritt 1: Das Gleichungssystem
Ausgangssituation: Zwei lineare Gleichungen
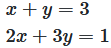
Abbildung 1: Das zu lösende Gleichungssystem
Schritt 2: Umwandlung in Matrixform
Durch Anwendung der Matrizenmultiplikationsregel können wir das System als Matrixgleichung schreiben:
A · X = B
wobei A die Koeffizientenmatrix ist, X der Lösungsvektor, und B die Konstanten sind.
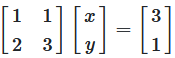
Abbildung 2: Das Gleichungssystem in Matrixform
Identifikation der Matrizen
Koeffizientenmatrix A
[1, 1]
[2, 3]
Die Koeffizienten der Variablen
Lösungsvektor X
[x]
[y]
Die gesuchten Variablen
Ergebnis B
[3]
[1]
Die konstanten Terme
Lösung durch Matrixinversion
Genau wie bei Zahlen können wir eine Matrixgleichung durch Inversion lösen:
Schritt 1: Bestimmung der Inversen
Wenn die Koeffizientenmatrix A invertierbar ist, können wir beide Seiten mit A⁻¹ multiplizieren:
A · X = B
A⁻¹ · A · X = A⁻¹ · B
I · X = A⁻¹ · B
X = A⁻¹ · B
Schritt 2: Berechnung der Inversen für unser Beispiel
Inverse der Koeffizientenmatrix
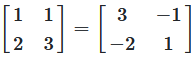
Abbildung 3: Die Inverse der Koeffizientenmatrix
Schritt 3: Multiplikation mit B und Lösung
Berechnung des Lösungsvektors
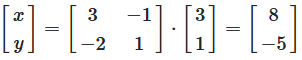
Abbildung 4: Berechnung der Lösung
Schritt 4: Verifikation
Überprüfung der Lösung
Allgemeines n×n Gleichungssystem
Das Verfahren funktioniert für beliebig große Systeme:
n Gleichungen mit n Unbekannten:
a₁₁x₁ + a₁₂x₂ + ... + a₁ₙxₙ = b₁
a₂₁x₁ + a₂₂x₂ + ... + a₂ₙxₙ = b₂
...
aₙ₁x₁ + aₙ₂x₂ + ... + aₙₙxₙ = bₙ
Matrixform: A · X = B, wobei X = A⁻¹ · B
Beispiel: 3×3 System
Lösung eines 3×3 Gleichungssystems
Wann funktioniert das Verfahren?
Das Matrixverfahren zur Lösung von Gleichungssystemen funktioniert nur unter bestimmten Bedingungen:
- Quadratische Matrix: A muss n × n sein (gleich viele Gleichungen wie Unbekannte)
- Nicht-singulär: det(A) ≠ 0 (Matrix muss invertierbar sein)
- Eindeutige Lösung: Wenn diese Bedingungen erfüllt sind, gibt es genau eine Lösung
Spezialfälle
| Fall | Bedingung | Lösungszahl |
|---|---|---|
| Eindeutige Lösung | det(A) ≠ 0 (Matrix invertierbar) | Genau eine Lösung ✓ |
| Keine Lösung | det(A) = 0 und Widerspruch in B | Keine Lösung ✗ |
| Unendlich viele Lösungen | det(A) = 0 aber konsistentes System | Unendlich viele Lösungen |
Wenn det(A) = 0 (singuläre Matrix), kann das System keine eindeutige Lösung haben. Die Matrix ist nicht invertierbar und das Verfahren funktioniert nicht!
Verschiedene Lösungsmethoden
Es gibt mehrere Möglichkeiten, lineare Gleichungssysteme mit Matrizen zu lösen:
Matrixinversion
X = A⁻¹ · B
Berechne die Inverse und multipliziere. Gut wenn A⁻¹ bereits bekannt.
Cramer-Regel
xᵢ = det(Aᵢ) / det(A)
Hilfreich für theoretische Überlegungen. Ineffizient für große Systeme.
Gauß-Jordan Elimination
Zeilenoperationen auf [A | B]
Standard-Methode. Effizient und numerisch stabil für praktische Probleme.
Gauß-Jordan Elimination ist die Standard-Methode für praktische Anwendungen, da sie am effizientesten ist und numerisch stabil arbeitet.
Praktische Anwendungen
Lineare Gleichungssysteme treten in vielen praktischen Problemen auf:
- Elektrotechnik: Kirchhoffsche Gesetze für komplexe Stromkreise
- Mechanik: Kräftegleichgewicht in Strukturen
- Chemie: Ausgleich chemischer Gleichungen
- Wirtschaft: Lineare Optimierung und Input-Output-Modelle
- Physik: Bewegungsgleichungen und Feldgleichungen
- Computergrafik: 3D-Transformationen und Rendering
Tipps und häufige Fehler
- Determinante prüfen: Berechne zuerst det(A), um zu testen ob Inversion möglich ist
- Matrixform korrekt: Achte darauf, dass A die Koeffizienten und B die Konstanten enthält
- Multiplikationsreihenfolge: Beachte, dass Matrizenmultiplikation nicht kommutativ ist
- Verifikation: Überprüfe die Lösung durch Einsetzen in die Original-Gleichungen
- Methode wählen: Für große Systeme Gauß-Jordan statt Inversion verwenden
- FALSCH: Koeffizientenmatrix singulär ignorieren | RICHTIG: Testen ob det(A) ≠ 0
- FALSCH: Gleichungen falsch in Matrix umwandeln | RICHTIG: Systematisch Koeffizienten in A, Konstanten in B
- FALSCH: B · A⁻¹ statt A⁻¹ · B | RICHTIG: Beachte Multiplikationsreihenfolge
- FALSCH: Lösung nicht überprüfen | RICHTIG: Immer in Original-Gleichungen einsetzen
|
|