Kegel Rechner
Rechner und Formeln zur Berechnung der Flächen und des Volumens eines Kegels
Kegel Rechner
Der Gerade Kreiskegel
Der gerade Kreiskegel ist ein Rotationskörper mit einer kreisförmigen Grundfläche und einer Spitze.
Kegel Eigenschaften
Der gerade Kreiskegel: Rotationskörper um die Höhenachse
Kegel Struktur
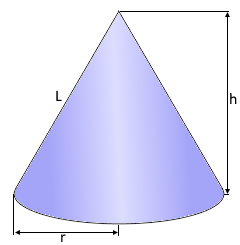
Der gerade Kreiskegel mit perfekter Symmetrie.
Kreisförmige Grundfläche und Spitze.
|
|
Was ist ein gerader Kreiskegel?
Der gerade Kreiskegel ist ein faszinierender Rotationskörper:
- Definition: Rotationskörper mit kreisförmiger Basis
- Achse: Senkrecht zur Grundfläche durch das Zentrum
- Spitze: Einziger Punkt auf der Achse
- Mantelfläche: Gekrümmte Oberfläche
- Grundfläche: Kreisförmige Basis
- Mantellinie: Gerade von Spitze zum Rand
Geometrische Eigenschaften des Kegels
Der gerade Kreiskegel zeigt bemerkenswerte geometrische Eigenschaften:
Grundparameter
- Radius (r): Radius der Grundfläche
- Höhe (h): Abstand Spitze zur Basis
- Mantellinie (L): √(h² + r²)
- Umfang (P): 2πr
Besondere Eigenschaften
- Rotationskörper: Um die Höhenachse
- Kegelschnitte: Kreis, Ellipse, Parabel, Hyperbel
- Ähnlichkeit: Alle Querschnitte sind ähnlich
- Pythagoras: L² = h² + r²
Mathematische Beziehungen
Der gerade Kreiskegel folgt eleganten mathematischen Gesetzen:
Volumen-Formel
Ein Drittel des Zylindervolumens. Elegant und fundamental.
Oberflächen-Formel
Summe aus Grundfläche und Mantelfläche. Pythagoras für Mantellinie.
Anwendungen des Kegels
Kegel finden Anwendung in verschiedenen Bereichen:
Architektur & Bauwesen
- Dächer und Türme
- Trichterförmige Strukturen
- Säulen und Säulenkopfstücke
- Dekorative Elemente
Industrie & Technik
- Trichter und Silos
- Ventile und Düsen
- Lautsprecher und Hörner
- Kegel- und Kegelräder
Bildung & Wissenschaft
- Geometrie-Unterricht
- Volumen- und Flächenberechnungen
- Kegelschnitt-Studien
- Rotationskörper-Demonstration
Alltag & Natur
- Eistüten und Waffeln
- Verkehrshütchen
- Vulkane und Berge
- Zapfen und Samen
Formeln zur Berechnung von Kegel
Basis Radius (r)
Radius aus der Grundfläche berechnen
Basis Umfang (P)
Umfang der kreisförmigen Grundfläche
Höhe (h)
Höhe aus Mantellinie oder Volumen
Mantelhöhe (L)
Pythagoras für die Mantellinie
Basisfläche (A)
Kreisfläche der Grundfläche
Mantelfläche (SL)
Mantelfläche ohne Grundfläche
Oberfläche (S)
Mantelfläche plus Grundfläche
Volumen (V)
Ein Drittel des entsprechenden Zylindervolumens
Berechnungsbeispiel für einen Kegel
Gegeben
Gesucht: Alle Eigenschaften des geraden Kreiskegels
1. Grundfläche-Berechnung
Für r = 10:
\[A = r^2 \cdot \pi\] \[A = 10^2 \cdot \pi = 100\pi\] \[A ≈ 314.16\]Die Grundfläche beträgt etwa 314.16 Flächeneinheiten
2. Volumen-Berechnung
Für r = 10, h = 5:
\[V = \frac{r^2 \cdot \pi \cdot h}{3}\] \[V = \frac{100\pi \cdot 5}{3} = \frac{500\pi}{3}\] \[V ≈ 523.60\]Das Volumen beträgt etwa 523.60 Volumeneinheiten
3. Mantellinie-Berechnung
Für r = 10, h = 5:
\[L = \sqrt{h^2 + r^2}\] \[L = \sqrt{5^2 + 10^2} = \sqrt{125}\] \[L ≈ 11.18\]Die Mantellinie beträgt etwa 11.18 Längeneinheiten
4. Oberfläche-Berechnung
Mantelfläche + Grundfläche:
\[S_L = \pi \cdot r \cdot L ≈ \pi \cdot 10 \cdot 11.18 ≈ 351.20\] \[S = S_L + A ≈ 351.20 + 314.16\] \[S ≈ 665.36\]Die Gesamtoberfläche beträgt etwa 665.36 Flächeneinheiten
5. Der perfekte Kegel
Der gerade Kreiskegel mit perfekter Rotationssymmetrie
Der gerade Kreiskegel: Perfektion der Rotation
Der gerade Kreiskegel ist einer der fundamentalsten Rotationskörper der Geometrie und verkörpert die Eleganz der mathematischen Perfektion. Entstanden durch die Rotation eines rechtwinkligen Dreiecks um eine seiner Katheten, vereint der Kegel in seiner Form die Einfachheit des Kreises mit der Dynamik der linearen Verjüngung. Seine mathematische Schönheit zeigt sich in den eleganten Beziehungen zwischen Radius, Höhe und Mantellinie, die durch den Satz des Pythagoras miteinander verknüpft sind und zu den fundamentalen Formeln für Volumen und Oberfläche führen.
Die Geometrie der Rotation
Der gerade Kreiskegel demonstriert die Kraft der Rotationssymmetrie:
- Rotationskörper: Entstanden durch Rotation um die Höhenachse
- Kreisförmige Basis: Perfekte Kreisscheibe als Grundfläche
- Konische Verjüngung: Gleichmäßige Verengung zur Spitze
- Pythagoras-Beziehung: L² = h² + r² verbindet alle Dimensionen
- Kegelschnitte: Erzeugt alle klassischen Kurven
- Ähnlichkeit: Alle Horizontalschnitte sind ähnliche Kreise
- Universalität: Grundform für unzählige Anwendungen
Mathematische Eleganz
Volumen-Perfektion
Das Kegelvolumen ist exakt ein Drittel des entsprechenden Zylindervolumens – eine der elegantesten Beziehungen der Geometrie.
Oberflächen-Harmonie
Die Mantelfläche folgt der einfachen Formel πrL, während die Gesamtoberfläche durch Addition der Grundfläche entsteht.
Kegelschnitt-Magie
Schnitte durch den Kegel erzeugen alle klassischen Kurven: Kreis, Ellipse, Parabel und Hyperbel – die Grundlagen der analytischen Geometrie.
Praktische Universalität
Von der Natur bis zur Technik – der Kegel ist überall: in Vulkanen, Trichtern, Dächer und unzähligen technischen Anwendungen.
Zusammenfassung
Der gerade Kreiskegel steht als Symbol für die Perfektion der Rotationsgeometrie und die Eleganz mathematischer Beziehungen. Seine einfache Entstehung durch Rotation eines Dreiecks führt zu einer Fülle faszinierender Eigenschaften, von den fundamentalen Volumen- und Oberflächenformeln bis hin zu den klassischen Kegelschnitten. In der Praxis findet der Kegel unzählige Anwendungen, von architektonischen Meisterwerken bis zu alltäglichen Gegenständen. Als Brücke zwischen der reinen Mathematik und der angewandten Geometrie bleibt der Kegel ein faszinierendes Beispiel für die Schönheit und Nützlichkeit geometrischer Formen. Seine Universalität und mathematische Eleganz machen ihn zu einem der wichtigsten Rotationskörper der Geometrie.
|
|
|
|