Calculate Koch Curve
Online calculator and formulas for calculating the Koch Curve - Fractal Snowflake
Koch Curve Calculator
Fractal Koch Curve
Calculates the fractal properties of the Koch Curve after n iterations - also known as the Koch Snowflake.
Visualization
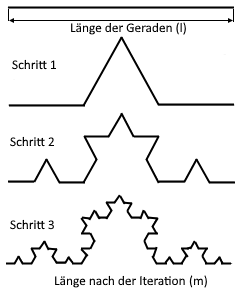
The graphic shows the iterative construction of the Koch Curve through tripartition and triangle construction.
Each iteration increases the complexity and length of the fractal curve.
|
|
What is the Koch Curve?
The Koch Curve is one of the most famous fractal curves in mathematics:
- Fractal: Self-similar, infinitely detailed structure
- Continuous: Connected everywhere, but nowhere differentiable
- Snowflake: Three Koch Curves form the Koch Snowflake
- Iterative: Created by repeated application of a rule
- Infinite length: Bounded area, but infinite perimeter
- Dimension: Fractal dimension between 1 and 2
Construction of the Koch Curve
The Koch Curve is created by iterative application of a simple construction rule:
Step 1: Tripartition
Each line segment is divided into three equal parts. The middle third is removed.
Step 2: Build triangle
An equilateral triangle is erected over the gap, whose base is then removed.
Fractal Properties
The Koch Curve shows typical fractal properties:
Self-similarity
Each part looks like the whole, just smaller
Infinite length
The length grows with each iteration by factor 4/3
Understanding the Iteration Process
With each iteration, new details emerge and the properties change:
n = 0
Straight line
Length: l
4 × 1 = 1 segment
n = 1
First triangle
Length: 4l/3
4 × 1 = 4 segments
n = 2
Four triangles
Length: 16l/9
4 × 4 = 16 segments
Koch Curve Formulas
Length after n iterations
The length grows exponentially with each iteration
Height of Koch Curve
Height of the first triangle
Inverse formula for length
Original length from iteration length
Length from height
Original length from given height
Fractal dimension
Hausdorff dimension of the Koch Curve
Symbols and Notations
- l: Length of the original line
- h: Height of the first triangle
- m: Length after n iterations
- n: Number of iterations
- D: Fractal dimension
- 4/3: Length growth factor
Example
Example Calculation
1. Calculate height
Height of the first triangle
2. Length after 3 iterations
More than double the length!
3. Count segments
Exponential growth of complexity
Properties
- Self-similar: Each part is a miniature of the whole
- Infinite: Tends toward infinite length
- Fractal: Dimension ≈ 1.26
The Koch Curve - Understanding Fractal Geometry
The Koch Curve, named after Swedish mathematician Helge von Koch (1904), is one of the most famous fractal curves and a prime example of the fascinating properties of fractal geometry. It is continuous everywhere but differentiable nowhere and has a fractal dimension between 1 and 2.
Historical Background
The Koch Curve was introduced in 1904 by Helge von Koch as an example of a continuous but non-differentiable curve. It was one of the first formally described fractal objects, long before the term "fractal" was coined by Benoit Mandelbrot.
Construction Principle
The construction of the Koch Curve follows a simple but powerful principle:
- Starting line: Begin with a straight line of length l
- Tripartition: The line is divided into three equal parts
- Removal: The middle third is removed
- Triangle: An equilateral triangle is erected over the resulting gap
- Iteration: This process is applied to each new line segment
Mathematical Properties
Exponential Length Growth
The length grows with each iteration by a factor of 4/3, leading to infinite length.
Fractal Dimension
The Hausdorff dimension is log(4)/log(3) ≈ 1.26, between line and surface.
Self-similarity
Each part of the curve is a scaled copy of the whole - perfect self-similarity.
Non-differentiability
No unique tangent exists at any point - the curve has "corners" everywhere.
The Koch Snowflake
When three Koch Curves are joined to form a closed triangle, the famous Koch Snowflake is created. This has the paradoxical property of having finite area with infinite perimeter.
Applications and Significance
The Koch Curve and its relatives find applications in various fields:
- Physics: Modeling coastlines, surface roughness
- Computer graphics: Generation of natural-looking structures
- Antenna technology: Fractal antennas with compact design
- Biology: Modeling blood vessels, bronchi
- Economics: Analysis of market fluctuations
- Art: Fractal art and design
Related Fractals
Cantor Set
One-dimensional fractal through iterative tripartition and middle removal.
Sierpinski Triangle
Two-dimensional fractal with similar construction logic.
Dragon Curve
Fractal curve through repeated 90° folding.
Mandelbrot Set
The most famous fractal, based on complex numbers.
Philosophical Significance
The Koch Curve illustrates important concepts of modern mathematics and philosophy:
- Paradoxes: Finite area with infinite perimeter
- Scale independence: Structures look the same at all magnification levels
- Complexity from simplicity: Simple rules generate infinite complexity
- Limits: What happens at the transition to infinity?
Practical Calculation
For practical applications, the Koch Curve is approximated after a finite number of iterations. After just a few iterations (n=3-5), the characteristic properties are clearly visible, while computation time remains manageable.
|
|
|
|