Calculate Helix
Online calculator and formulas for calculating a helix curve
Helix Calculator
Calculate Helix Curve
Calculates pitch, curvature, torsion and arc length of a three-dimensional helical curve.
Visualization
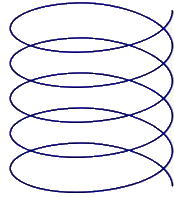
The graphic shows a helix as a three-dimensional spiral curve around a cylinder.
The helix is created by simultaneous rotation and translation along the axis.
|
|
What is a Helix?
A helix (spiral curve) is a three-dimensional curve that winds spirally around an axis:
- Rotation + Translation: Simultaneous rotation and displacement
- Constant pitch: Uniform height gain per revolution
- Cylindrical form: Winds around an imaginary cylinder
- Unwrapping: Results in a straight line when unwrapped
- Applications: Spiral staircase, thread, DNA structure
- Properties: Pitch, curvature, torsion
Curvature and Pitch
The geometric properties of a helix are described by various parameters:
Pitch k
Ratio of turn height to circumference
Curvature κ
Measure of the bending of the curve
Torsion and Twist
The torsion describes how strongly the helix twists out of the plane:
Torsion ω
Measure of spatial twist
Meaning
- ω = 0: Planar curve
- ω > 0: Spatial twist
- Large ω: Strong helical twist
Calculate Arc Length
The arc length is the actual length of the helix curve:
Arc length s
Length for t turns
Derivation
From circumference and height per turn
Helix Formulas Overview
Parametric Representation of a Helix
Parametric equations with parameter t (angle)
Pitch
Ratio of turn height to circumference
Curvature
Local bending of the curve
Torsion
Spatial twist
Arc Length
Total length for t turns
Symbols and Notations
- r: Radius of the cylinder
- h: Height of one turn
- t: Number of turns
- k: Pitch of the helix
- κ (kappa): Curvature
- ω (omega): Torsion
- s: Arc length
- π: Pi (≈ 3.14159)
Example
Example Calculation
1. Calculate pitch
Very gentle pitch
2. Calculate curvature
Moderate curvature
3. Calculate torsion
Low twist
4. Arc length
Total length of the helix
The Helix in Mathematics and Engineering
A helix (plural: helices) is a three-dimensional curve that winds spirally around an axis. It is created by the combination of uniform rotation around an axis with uniform translation along that axis. The helix is a fundamental geometric object with diverse applications in nature and technology.
Mathematical Definition
A helix can be represented parametrically as:
Where r is the radius, h is the pitch height per full revolution and t is the parameter (angle).
Geometric Properties
Pitch
The ratio of turn height to circumference determines how steeply the helix rises.
Curvature
Describes how strongly the curve deviates from a straight line.
Torsion
Measures the spatial twist of the curve out of the plane.
Arc Length
The actual length of the wound curve, always greater than the height.
Applications in Practice
Helix structures are found everywhere in nature and technology:
- Architecture: Spiral staircases, helical ramps, towers
- Mechanical engineering: Threads, screws, twist drills, springs
- Biology: DNA double helix, protein structures, snail shells
- Physics: Magnetic field lines, particle paths in accelerators
- Chemistry: Molecular structures, crystal lattices
- Technology: Pipelines, cables, transport screws
Special Properties
Unwrapping
When a helix is "unrolled" on a cylinder surface, a straight line is created.
Constant Pitch
The pitch remains constant over the entire curve, unlike other spirals.
Chirality
Helices can be right-handed or left-handed (right or left thread).
Scalability
Helix structures work at all size scales, from molecular to macroscopic.
Related Curves
The helix belongs to a family of related curves:
- Archimedean spiral: Spiral in the plane with constant radius growth
- Logarithmic spiral: Spiral with constant growth factor
- Conical helix: Helix on a cone instead of cylinder
- Spherical spiral: Spiral on a sphere surface
Calculation and Optimization
In practice, optimization of helix parameters is often important:
- Threads: Optimal pitch for strength and functionality
- Stairs: Comfortable pitch for users
- Springs: Stiffness and elasticity through helix parameters
- Drills: Chip removal and cutting performance
|
|
|
|