Pointed Pillar Calculator
Calculator and formulas for calculating a pointed pillar (truncated cone with cone)
Pointed Pillar Calculator
The Pointed Pillar
The pointed pillar is a composite solid consisting of a truncated cone base with a conical top.
Pointed Pillar Properties
The composite solid: Truncated cone base with conical top
Pointed Pillar Structure
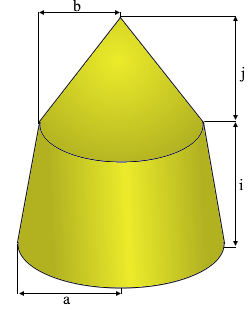
The pointed pillar with composite geometry.
Truncated cone base with conical top.
|
|
What is a pointed pillar?
The pointed pillar is a fascinating composite three-dimensional solid:
- Definition: Composite of truncated cone base and conical top
- Base: Truncated cone with circular bottom and top
- Top: Complete cone on the truncated section
- Structure: Pillar-like appearance with pointed top
- Transition: Smooth connection at radius b
- Applications: Architectural and decorative elements
Geometric Properties of the Pointed Pillar
The pointed pillar demonstrates complex composite geometry:
Basic Parameters
- Base radius (a): Radius of the bottom circle
- Transition radius (b): Radius where cone begins
- Base height (i): Height of truncated cone section
- Cone height (j): Height of the conical top
Special Properties
- Composite solid: Two geometric shapes combined
- Smooth transition: Continuous surface at junction
- Complex formulas: Sum of truncated cone and cone
- Architectural use: Common in columns and pillars
Mathematical Relationships
The pointed pillar follows complex composite mathematical laws:
Volume Formula
Sum of truncated cone and cone volumes. Complex but systematic approach.
Surface Formula
Base area plus lateral surfaces. Complex slant height calculations.
Applications of the Pointed Pillar
Pointed pillars find applications in various architectural and engineering contexts:
Architecture & Construction
- Classical column capitals
- Decorative pillar tops
- Monument design
- Structural column elements
Engineering & Manufacturing
- Machine components
- Specialized fasteners
- Pressure vessel heads
- Flow control elements
Art & Design
- Sculptural elements
- Decorative objects
- Garden ornaments
- Artistic installations
Education & Mathematics
- Composite solid studies
- Volume calculation exercises
- Surface area problems
- 3D geometry demonstrations
Formulas for Calculating Pointed Pillars
Base Area (A)
Area of the circular bottom base
Lateral Area (L)
Combined lateral surfaces of truncated cone and cone
Surface Area (S)
Base area plus lateral area
Volume (V)
Sum of truncated cone and cone volumes
Component Breakdown
\(V_1 = \frac{\pi i}{3}(a^2 + ab + b^2)\)
\(V_2 = \frac{\pi b^2 j}{3}\)
The pointed pillar volume is the sum: V = V₁ + V₂
Calculation Example for a Pointed Pillar
Given
Find: All properties of the pointed pillar
1. Base Area Calculation
For a = 4:
\[A = a^2 \cdot \pi\] \[A = 4^2 \cdot \pi = 16\pi\] \[A ≈ 50.27\]The base area is approximately 50.27 square units
2. Volume Calculation
Using the composite formula:
\[V = \frac{\pi}{3}[i(a^2 + ab + b^2) + b^2 j]\] \[V = \frac{\pi}{3}[4(16 + 12 + 9) + 9 \cdot 3]\] \[V = \frac{\pi}{3}[148 + 27] = \frac{175\pi}{3} ≈ 183.26\]The volume is approximately 183.26 cubic units
3. Lateral Area Calculation
Using the complex lateral formula:
\[L = [(a+b)\sqrt{(a-b)^2+i^2} + b\sqrt{j^2+b^2}]\pi\] \[L = [7\sqrt{1+16} + 3\sqrt{9+9}]\pi\] \[L = [7\sqrt{17} + 3\sqrt{18}]\pi ≈ 124.34\]The lateral area is approximately 124.34 square units
4. Total Surface Calculation
Base area + lateral area:
\[S = A + L\] \[S ≈ 50.27 + 124.34\] \[S ≈ 174.61\]The total surface is approximately 174.61 square units
5. The Perfect Pointed Pillar
The pointed pillar with perfect composite geometry
Volume Components Breakdown
Truncated Cone Volume:
V₁ = (π/3) × 4 × (16 + 12 + 9) = (148π/3) ≈ 154.99
Cone Volume:
V₂ = (π/3) × 9 × 3 = 9π ≈ 28.27
Total Volume: V = V₁ + V₂ ≈ 154.99 + 28.27 = 183.26 cubic units
The Pointed Pillar: Composite Geometry in Architectural Form
The pointed pillar represents a sophisticated example of composite solid geometry, where the practical needs of architecture meet the mathematical elegance of combined geometric forms. By uniting a truncated cone base with a conical top, this structure creates a form that is both structurally sound and aesthetically pleasing. The pointed pillar demonstrates how complex engineering problems can be solved through the thoughtful combination of simpler geometric elements, showcasing the power of composite mathematical modeling in real-world applications. Its study bridges pure geometry with practical architectural and engineering considerations.
The Geometry of Composite Construction
The pointed pillar demonstrates the elegance of composite geometric construction:
- Composite structure: Two distinct geometric solids combined seamlessly
- Smooth transition: Continuous surface at the junction between truncated cone and cone
- Complex calculations: Formulas that account for both components
- Architectural functionality: Combines structural stability with aesthetic appeal
- Parametric design: Four independent parameters allow flexible proportions
- Mathematical synthesis: Volume and surface formulas combine multiple geometric principles
- Practical versatility: Adaptable to various architectural and engineering needs
Mathematical Sophistication
Composite Volume Formula
The volume calculation elegantly combines truncated cone and cone formulas, demonstrating how complex solids can be analyzed through decomposition.
Complex Surface Calculation
The lateral surface area formula accounts for both the truncated cone's slant height and the cone's slant height, requiring sophisticated geometric analysis.
Architectural Applications
From classical columns to modern structural elements, the pointed pillar provides both functional strength and visual appeal in architectural design.
Engineering Versatility
The four-parameter design allows engineers to optimize proportions for specific structural, aesthetic, or manufacturing requirements.
Summary
The pointed pillar stands as a testament to the power of composite geometric design and the practical application of mathematical principles in architectural form. Its sophisticated combination of truncated cone and cone creates a structure that serves both functional and aesthetic purposes while demonstrating advanced mathematical concepts. From ancient classical architecture to modern engineering applications, the pointed pillar continues to showcase how thoughtful geometric combination can create forms of enduring beauty and utility. The mathematical analysis of this composite solid reveals the deep connections between pure geometry, practical engineering, and architectural design, making it an excellent example of applied mathematics in the built environment.