Double Cone Calculator
Calculator and formulas for calculating a double cone (bicone)
Double Cone Calculator
The Double Cone (Bicone)
The double cone is a rotational solid consisting of two cones joined at their bases.
Double Cone Properties
The bicone: Two identical cones joined base-to-base
Double Cone Structure
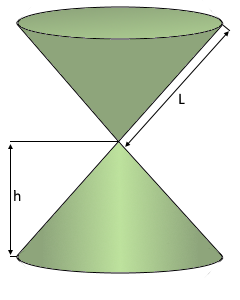
The double cone with perfect bilateral symmetry.
Two cones sharing a circular base.
|
|
What is a double cone?
The double cone (bicone) is a fascinating rotational solid:
- Definition: Two identical cones joined base-to-base
- Symmetry: Perfect bilateral symmetry around the base
- Apexes: Two apex points on opposite sides
- Shape: Hourglass or diamond-like profile
- Rotation: Symmetric around the central axis
- Base: Shared circular foundation
Geometric Properties of the Double Cone
The double cone demonstrates remarkable geometric properties:
Basic Parameters
- Radius (r): Radius of the shared circular base
- Height (h): Height of each individual cone
- Total height: 2h (sum of both cone heights)
- Slant height (L): √(h² + r²)
Special Properties
- Bilateral symmetry: Mirror image across base plane
- Rotational solid: Around the central axis
- Double volume: Exactly twice a single cone
- Hourglass profile: Characteristic narrow waist
Mathematical Relationships
The double cone follows elegant mathematical laws:
Volume Formula
Exactly twice the volume of a single cone. Simple multiplication factor.
Surface Formula
Two lateral surfaces plus the shared base. No doubling of the base area.
Applications of the Double Cone
Double cones find applications in various fields:
Engineering & Technology
- Hourglass structures
- Flow restrictors and nozzles
- Pressure vessels
- Acoustic horns
Science & Research
- Crystal growth chambers
- Optics and light cones
- Particle physics detectors
- Mathematical modeling
Architecture & Design
- Decorative elements
- Sculptural forms
- Structural components
- Artistic installations
Practical Applications
- Sand timers and hourglasses
- Separation funnels
- Centrifugal separators
- Decorative objects
Formulas for Calculating Double Cones
Base Area (A)
Area of the shared circular base
Slant Length (L)
Pythagoras for the slant line of each cone
Both Lateral Areas (SL)
Combined lateral surface of both cones
Total Surface (S)
Two base areas plus lateral surfaces
Volume (V)
Exactly twice the volume of a single cone
Calculation Example for a Double Cone
Given
Find: All properties of the double cone
1. Base Area Calculation
For r = 5:
\[A = r^2 \cdot \pi\] \[A = 5^2 \cdot \pi = 25\pi\] \[A ≈ 78.54\]The base area is approximately 78.54 square units
2. Slant Height Calculation
For r = 5, h = 6:
\[L = \sqrt{r^2 + h^2}\] \[L = \sqrt{5^2 + 6^2} = \sqrt{61}\] \[L ≈ 7.81\]The slant height is approximately 7.81 length units
3. Volume Calculation
For r = 5, h = 6:
\[V = \frac{2}{3} \cdot r^2 \cdot \pi \cdot h\] \[V = \frac{2}{3} \cdot 25\pi \cdot 6 = 100\pi\] \[V ≈ 314.16\]The volume is approximately 314.16 cubic units
4. Total Surface Calculation
Lateral surfaces + base areas:
\[S_L = 2 \cdot \pi \cdot r \cdot L ≈ 2 \cdot \pi \cdot 5 \cdot 7.81 ≈ 245.04\] \[S = 2A + S_L ≈ 2 \cdot 78.54 + 245.04\] \[S ≈ 402.12\]The total surface is approximately 402.12 square units
5. The Perfect Double Cone
The double cone with perfect bilateral symmetry
The Double Cone: Symmetry in Perfect Balance
The double cone (bicone) represents one of the most elegant examples of bilateral symmetry in three-dimensional geometry. By joining two identical cones at their bases, this remarkable solid creates a form that embodies perfect balance and mathematical harmony. The double cone's distinctive hourglass profile has fascinated mathematicians, architects, and engineers for centuries, serving as both a pure geometric form and a practical solution in countless applications. Its mathematical beauty lies in the simple relationships that govern its properties, where doubling creates elegance rather than complexity.
The Geometry of Bilateral Symmetry
The double cone demonstrates the power of symmetrical construction:
- Perfect symmetry: Mirror image across the shared base plane
- Rotational solid: Created by rotation around the central axis
- Hourglass profile: Characteristic narrow waist at the base
- Dual apexes: Two points of convergence on opposite sides
- Simple multiplication: Most properties are exactly double
- Shared foundation: Single circular base supports both cones
- Versatile form: Natural shape for many applications
Mathematical Elegance
Volume Simplicity
The double cone volume is exactly twice that of a single cone – one of the most intuitive relationships in solid geometry.
Surface Harmony
The surface area combines two lateral surfaces with shared base areas, creating a balanced formula structure.
Practical Versatility
From hourglasses to industrial separators, the bicone shape provides optimal flow characteristics and structural stability.
Aesthetic Appeal
The hourglass profile creates visual tension and balance, making it a favorite form in art and architecture.
Summary
The double cone stands as a testament to the elegance of symmetrical geometry and the power of simple multiplication in mathematical relationships. Its creation through the union of two identical cones results in a form that is both visually striking and mathematically pure. From the ancient hourglass to modern industrial applications, the bicone continues to serve as a bridge between pure geometry and practical utility. Its perfect bilateral symmetry and intuitive mathematical properties make it an excellent example of how simple geometric principles can create forms of enduring beauty and functionality. The double cone reminds us that sometimes the most elegant solutions come from the thoughtful combination of familiar elements.