Truncated Elliptic Cone Calculator
Calculator and formulas for calculating a truncated elliptic cone (elliptical frustum)
Truncated Elliptic Cone Calculator
The Truncated Elliptic Cone
The truncated elliptic cone is a section of an elliptic cone with elliptical bases of different sizes.
Elliptical Frustum Properties
The elliptical frustum: Complex geometry with elliptical cross-sections
Elliptical Frustum Structure
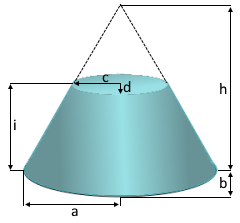
The truncated elliptic cone with oval bases.
Large ellipse bottom, smaller ellipse top.
|
|
What is a truncated elliptic cone?
The truncated elliptic cone (elliptical frustum) is an advanced three-dimensional solid:
- Definition: Section of an elliptic cone with top cut off
- Base: Large ellipse with semi-axes a and b
- Top: Smaller ellipse with semi-axes c and d
- Relationship: Top axes proportional to bottom axes
- Surface: Complex elliptical lateral surface
- Applications: Advanced engineering and design
Geometric Properties of the Elliptical Frustum
The truncated elliptic cone demonstrates highly advanced geometric relationships:
Basic Parameters
- Bottom semi-axes (a, b): Define the large elliptical base
- Cone height (h): Height of the complete elliptic cone
- Truncated height (i): Height of the frustum section
- Remaining height (j): j = h - i
Special Properties
- Proportional scaling: Top ellipse scales with cone section
- Complex surface: Elliptical lateral surface integration
- Volume difference: Complete cone minus removed section
- Advanced calculations: Requires elliptic integral approximations
Mathematical Relationships
The truncated elliptic cone follows highly complex mathematical laws:
Volume Formula
Complete elliptic cone minus removed section. Elegant subtraction approach.
Surface Formula
Complex elliptical surface calculations. Requires advanced integral approximations.
Applications of the Elliptical Frustum
Truncated elliptic cones find specialized applications in advanced engineering:
Aerospace Engineering
- Advanced airframe sections
- Specialized nozzle designs
- Composite structural elements
- Aerodynamic transition pieces
Advanced Manufacturing
- Precision machine components
- Specialized flow channels
- High-tech pressure vessels
- Complex geometric transitions
Architectural Design
- Advanced structural elements
- Modern sculptural forms
- Complex geometric transitions
- Specialized decorative elements
Advanced Mathematics
- Complex 3D geometry studies
- Elliptic integral applications
- Advanced calculus problems
- Engineering mathematics research
Formulas for Calculating Truncated Elliptic Cones
Truncated Height (j)
Height of the removed top section
Base Area (A)
Area of the elliptical base
Top Semi-axis (c)
Large semi-axis of the top ellipse
Top Semi-axis (d)
Small semi-axis of the top ellipse
Volume (V)
Complete elliptic cone volume minus removed section volume
Total Surface (S)
Base area plus lateral surface area
Top Area (Atop)
Area of the elliptical top surface
Lateral Surface (M) - Approximation
Approximation using elliptic surface formulas (slightly below exact value)
Calculation Example for a Truncated Elliptic Cone
Given
Find: All properties of the truncated elliptic cone
1. Top Semi-axes Calculation
First find j = h - i = 6 - 4 = 2
\[c = \frac{a \cdot j}{h} = \frac{3 \cdot 2}{6} = 1\] \[d = \frac{b \cdot j}{h} = \frac{2 \cdot 2}{6} = \frac{2}{3} ≈ 0.67\]Top semi-axes: c = 1.0, d ≈ 0.67
2. Base Area Calculation
For a = 3, b = 2:
\[A = a \cdot b \cdot \pi\] \[A = 3 \cdot 2 \cdot \pi = 6\pi\] \[A ≈ 18.85\]The base area is approximately 18.85 square units
3. Volume Calculation
Using the difference formula:
\[V = \frac{\pi}{3}(h \cdot a \cdot b - j \cdot c \cdot d)\] \[V = \frac{\pi}{3}(6 \cdot 3 \cdot 2 - 2 \cdot 1 \cdot 0.67)\] \[V = \frac{\pi}{3}(36 - 1.33) ≈ 36.28\]The volume is approximately 36.28 cubic units
4. Lateral Surface Calculation
Using approximation formula:
Bottom contribution: 3√(4+36) + 2√(9+36) ≈ 27.31
Top contribution: 1√(0.44+4) + 0.67√(1+4) ≈ 3.61
\[M ≈ \frac{\pi}{2}(27.31 - 3.61) ≈ 37.20\]The lateral surface is approximately 37.20 square units
5. The Perfect Elliptical Frustum
The truncated elliptic cone with advanced elliptical geometry
Mathematical Complexity Note
The truncated elliptic cone represents one of the most mathematically complex geometric solids in practical use. The lateral surface calculation requires sophisticated elliptic integral approximations, as the exact solution involves elliptic integrals of the first and second kind. The proportional scaling relationship between the top and bottom ellipses (c/a = d/b = j/h) provides the geometric foundation for all calculations, but the surface area determination remains one of the most challenging problems in applied solid geometry.
The Truncated Elliptic Cone: Advanced Geometric Complexity
The truncated elliptic cone (elliptical frustum) represents the pinnacle of geometric complexity in practical solid geometry, combining the sophistication of elliptical cross-sections with the mathematical challenges of truncated solids. This remarkable shape demonstrates how the intersection of advanced mathematical concepts creates forms that push the boundaries of both theoretical understanding and practical application. The elliptical frustum requires the most sophisticated mathematical tools in solid geometry, from proportional scaling relationships to elliptic integral approximations, making it a fascinating subject for advanced mathematical study and cutting-edge engineering applications.
The Geometry of Elliptical Truncation
The truncated elliptic cone demonstrates the ultimate complexity of sectioned solids:
- Elliptical bases: Both top and bottom surfaces are ellipses with different dimensions
- Proportional scaling: Top ellipse dimensions scale proportionally with truncation
- Complex lateral surface: Curved elliptical surface requiring integral calculations
- Volume difference method: Complete cone minus removed section approach
- Elliptic integral approximations: Surface area requires advanced mathematical techniques
- Multi-parameter geometry: Four independent parameters define the complete shape
- Engineering challenges: Manufacturing and measurement complexity
Mathematical Sophistication
Elliptic Integral Requirements
The exact lateral surface area calculation requires elliptic integrals of the first and second kind, representing one of the most advanced applications of integral calculus in solid geometry.
Proportional Scaling Laws
The relationship c/a = d/b = j/h provides the fundamental geometric principle that governs all truncated elliptic cone calculations.
Advanced Engineering Applications
From aerospace nozzles to precision manufacturing, the elliptical frustum provides optimal solutions for the most demanding engineering challenges.
Computational Complexity
Modern CAD systems and numerical methods have made elliptical frustum calculations practical, opening new possibilities in advanced design and manufacturing.
Summary
The truncated elliptic cone stands as the ultimate expression of geometric complexity and mathematical sophistication in practical solid geometry. Its combination of elliptical cross-sections, proportional scaling relationships, and elliptic integral surface calculations creates a form that challenges both theoretical understanding and practical application. From the elegant proportional scaling laws that govern its geometry to the sophisticated elliptic integral approximations required for surface area calculations, the elliptical frustum represents the convergence of advanced mathematics and cutting-edge engineering. As computational methods continue to advance, the truncated elliptic cone will undoubtedly find increasing applications in fields demanding the highest levels of geometric precision and mathematical sophistication, making it a fascinating bridge between pure mathematical theory and practical engineering innovation.