Rounded Cone Calculator
Calculator and formulas for calculating a rounded cone (truncated cone with spherical cap)
Rounded Cone Calculator
The Rounded Cone
The rounded cone is a composite solid consisting of a truncated cone with a spherical cap.
Rounded Cone Properties
The composite solid: Truncated cone base with spherical cap top
Rounded Cone Structure
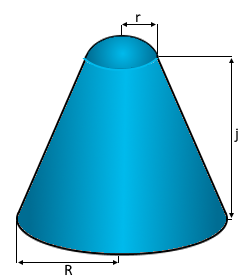
The rounded cone with spherical cap.
Truncated cone base with smooth spherical top.
|
|
What is a rounded cone?
The rounded cone is a sophisticated composite three-dimensional solid:
- Definition: Truncated cone with a spherical cap on top
- Base: Truncated cone with circular bottom and top
- Top: Spherical cap that smoothly connects to the truncated section
- Geometry: Complex blend of conical and spherical surfaces
- Transition: Smooth connection at the cap radius
- Applications: Aerodynamic and architectural uses
Geometric Properties of the Rounded Cone
The rounded cone demonstrates sophisticated composite geometry:
Basic Parameters
- Base radius (R): Radius of the truncated cone base
- Cap radius (r): Radius of the spherical cap
- Cone height (j): Height of truncated cone section
- Cap height (i): Height of the spherical cap (calculated)
Special Properties
- Composite solid: Truncated cone plus spherical cap
- Smooth transition: Tangential connection at junction
- Complex formulas: Trigonometric and spherical calculations
- Aerodynamic shape: Ideal for flow applications
Mathematical Relationships
The rounded cone follows complex mathematical laws:
Volume Formula
Sum of truncated cone and spherical cap volumes. Complex spherical geometry involved.
Surface Formula
Base area plus lateral surfaces. Involves cone base angle calculations.
Applications of the Rounded Cone
Rounded cones find applications in specialized engineering and design contexts:
Aerospace & Aerodynamics
- Aircraft nose cones
- Rocket fairing sections
- Streamlined components
- Wind tunnel models
Engineering & Manufacturing
- Pressure vessel heads
- Flow control devices
- Automotive components
- Specialized containers
Architecture & Design
- Dome connections
- Decorative elements
- Modern architectural forms
- Sculptural applications
Education & Research
- Advanced geometry studies
- Composite solid analysis
- Fluid dynamics research
- Engineering mathematics
Formulas for Calculating Rounded Cones
Cone Base Angle (α)
Angle at the base of the truncated cone
Height of Cap (i)
Height of the spherical cap section
Surface Area (S)
Lateral surface of truncated cone + base area + spherical cap surface
Volume (V)
Volume of truncated cone + volume of spherical cap
Total Height (h)
Sum of truncated cone height and cap height
Spherical Cap Volume
Standard spherical cap volume formula
Calculation Example for a Rounded Cone
Given
Find: All properties of the rounded cone
1. Cone Base Angle Calculation
For R = 4, r = 3, j = 4:
\[\alpha = \arccos\left(\frac{4-3}{\sqrt{4^2+(4-3)^2}}\right)\] \[\alpha = \arccos\left(\frac{1}{\sqrt{17}}\right)\] \[\alpha ≈ 1.326 \text{ rad} ≈ 75.96°\]The cone base angle is approximately 75.96°
2. Cap Height Calculation
Using the cap height formula:
\[i = \sqrt{\frac{r^2}{\frac{2}{1-\cos(\alpha)} - 1}}\] \[i = \sqrt{\frac{9}{\frac{2}{1-0.2425} - 1}}\] \[i ≈ 1.73\]The cap height is approximately 1.73 units
3. Volume Calculation
Truncated cone + spherical cap:
\[V_{cone} = \frac{\pi}{3} \cdot 4 \cdot (16 + 12 + 9) = \frac{148\pi}{3}\] \[V_{cap} = \frac{\pi \cdot 1.73^2}{3}(3 \cdot 3 - 1.73) ≈ 21.24\] \[V_{total} ≈ 154.99 + 21.24 = 176.23\]The total volume is approximately 176.23 cubic units
4. Surface Area Calculation
Base + lateral + cap surfaces:
\[S_{base} = \pi \cdot 16 = 16\pi ≈ 50.27\] \[S_{lateral} = 7\pi\sqrt{17} ≈ 90.72\] \[S_{cap} = \pi(9 + 2.99) ≈ 37.68\] \[S_{total} ≈ 178.67\]The total surface area is approximately 178.67 square units
5. The Perfect Rounded Cone
The rounded cone with perfect spherical cap integration
Mathematical Complexity Note
The rounded cone involves sophisticated mathematical relationships between trigonometry and spherical geometry. The cone base angle α determines the cap height through inverse trigonometric functions, while the volume calculation requires careful integration of both truncated cone and spherical cap geometries. This makes the rounded cone one of the most mathematically complex composite solids in practical engineering applications.
The Rounded Cone: Sophisticated Geometric Integration
The rounded cone represents one of the most sophisticated examples of composite solid geometry, seamlessly blending conical and spherical elements into a unified mathematical framework. This remarkable shape demonstrates the elegant complexity that emerges when classical geometric forms are integrated with advanced trigonometric relationships and spherical cap calculations. The rounded cone showcases the practical application of advanced mathematics in engineering design, where smooth aerodynamic transitions and structural optimization requirements demand precise geometric modeling. Its study bridges pure geometry, advanced calculus, and real-world engineering applications in aerospace, automotive, and architectural design.
The Geometry of Smooth Integration
The rounded cone demonstrates the sophistication of seamless geometric integration:
- Composite structure: Truncated cone base with spherical cap top
- Tangential connection: Smooth transition ensuring no sharp edges
- Trigonometric relationships: Cone base angle determines cap geometry
- Spherical cap integration: Complex volume and surface calculations
- Aerodynamic optimization: Ideal for fluid flow applications
- Mathematical sophistication: Requires advanced geometric analysis
- Engineering versatility: Perfect for specialized technical applications
Mathematical Elegance and Complexity
Trigonometric Foundation
The cone base angle α serves as the fundamental parameter that connects the truncated cone geometry with the spherical cap dimensions, requiring inverse trigonometric calculations.
Spherical Cap Complexity
The spherical cap calculations involve sophisticated relationships between radius, height, and volume that challenge traditional geometric analysis methods.
Engineering Applications
From aircraft nose cones to pressure vessel heads, the rounded cone provides optimal aerodynamic and structural properties for demanding engineering applications.
Mathematical Integration
The seamless blend of conical and spherical geometries demonstrates how advanced mathematics enables the creation of sophisticated engineering solutions.
Summary
The rounded cone stands as a testament to the power of advanced geometric integration and the practical application of sophisticated mathematical relationships in engineering design. Its seamless combination of truncated cone and spherical cap geometries creates a form that is both mathematically elegant and practically superior for aerodynamic and structural applications. The complex trigonometric and spherical relationships that govern its properties demonstrate how advanced mathematics enables the creation of optimized engineering solutions. From aerospace nose cones to architectural domes, the rounded cone continues to showcase the deep connection between mathematical sophistication and practical innovation, making it an excellent example of how geometric complexity can yield both theoretical insights and real-world engineering advantages.