Right Circular Cone Calculator
Calculator and formulas for calculating a right circular cone
Cone Calculator
The Right Circular Cone
The right circular cone is a rotational solid with a circular base and an apex.
Cone Properties
The right circular cone: Rotational solid around the height axis
Cone Structure
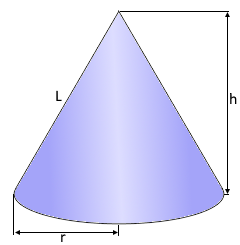
The right circular cone with perfect symmetry.
Circular base and apex point.
|
|
What is a right circular cone?
The right circular cone is a fascinating rotational solid:
- Definition: Rotational solid with circular base
- Axis: Perpendicular to the base through the center
- Apex: Single point on the axis
- Lateral surface: Curved outer surface
- Base: Circular foundation
- Slant line: Straight line from apex to edge
Geometric Properties of the Cone
The right circular cone demonstrates remarkable geometric properties:
Basic Parameters
- Radius (r): Radius of the base circle
- Height (h): Distance from apex to base
- Slant height (L): √(h² + r²)
- Perimeter (P): 2πr
Special Properties
- Rotational solid: Around the height axis
- Conic sections: Circle, ellipse, parabola, hyperbola
- Similarity: All cross-sections are similar
- Pythagoras: L² = h² + r²
Mathematical Relationships
The right circular cone follows elegant mathematical laws:
Volume Formula
One third of the cylinder volume. Elegant and fundamental.
Surface Formula
Sum of base area and lateral surface. Pythagoras for slant height.
Applications of the Cone
Cones find applications in various fields:
Architecture & Construction
- Roofs and towers
- Funnel-shaped structures
- Columns and capitals
- Decorative elements
Industry & Technology
- Funnels and silos
- Valves and nozzles
- Speakers and horns
- Cone and bevel gears
Education & Science
- Geometry lessons
- Volume and area calculations
- Conic section studies
- Rotational solid demonstrations
Everyday Life & Nature
- Ice cream cones and wafers
- Traffic cones
- Volcanoes and mountains
- Pine cones and seeds
Formulas for Calculating Cones
Base Radius (r)
Calculate radius from base area
Base Perimeter (P)
Perimeter of the circular base
Height (h)
Height from slant length or volume
Slant Height (L)
Pythagoras for the slant line
Base Area (A)
Circular area of the base
Lateral Surface (SL)
Lateral surface without base
Total Surface (S)
Lateral surface plus base area
Volume (V)
One third of the corresponding cylinder volume
Calculation Example for a Cone
Given
Find: All properties of the right circular cone
1. Base Area Calculation
For r = 10:
\[A = r^2 \cdot \pi\] \[A = 10^2 \cdot \pi = 100\pi\] \[A ≈ 314.16\]The base area is approximately 314.16 square units
2. Volume Calculation
For r = 10, h = 5:
\[V = \frac{r^2 \cdot \pi \cdot h}{3}\] \[V = \frac{100\pi \cdot 5}{3} = \frac{500\pi}{3}\] \[V ≈ 523.60\]The volume is approximately 523.60 cubic units
3. Slant Height Calculation
For r = 10, h = 5:
\[L = \sqrt{h^2 + r^2}\] \[L = \sqrt{5^2 + 10^2} = \sqrt{125}\] \[L ≈ 11.18\]The slant height is approximately 11.18 length units
4. Total Surface Calculation
Lateral surface + base area:
\[S_L = \pi \cdot r \cdot L ≈ \pi \cdot 10 \cdot 11.18 ≈ 351.20\] \[S = S_L + A ≈ 351.20 + 314.16\] \[S ≈ 665.36\]The total surface is approximately 665.36 square units
5. The Perfect Cone
The right circular cone with perfect rotational symmetry
The Right Circular Cone: Perfection of Rotation
The right circular cone stands as one of the most fundamental rotational solids in geometry, embodying the elegance of mathematical perfection. Created by rotating a right triangle around one of its legs, the cone unites the simplicity of the circle with the dynamics of linear tapering in its form. Its mathematical beauty is revealed in the elegant relationships between radius, height, and slant height, connected through the Pythagorean theorem and leading to the fundamental formulas for volume and surface area. From ancient Greek mathematics to modern engineering applications, the cone continues to serve as a cornerstone of three-dimensional geometry.
The Geometry of Rotation
The right circular cone demonstrates the power of rotational symmetry:
- Rotational solid: Created by rotation around the height axis
- Circular base: Perfect circular disc as foundation
- Conical tapering: Uniform narrowing to the apex
- Pythagorean relationship: L² = h² + r² connects all dimensions
- Conic sections: Generates all classical curves
- Similarity: All horizontal sections are similar circles
- Universality: Fundamental shape for countless applications
Mathematical Elegance
Volume Perfection
The cone volume is exactly one third of the corresponding cylinder volume – one of the most elegant relationships in geometry.
Surface Harmony
The lateral surface follows the simple formula πrL, while the total surface is created by adding the base area.
Conic Section Magic
Cuts through the cone create all classical curves: circle, ellipse, parabola, and hyperbola – the foundations of analytic geometry.
Practical Universality
From nature to technology – the cone is everywhere: in volcanoes, funnels, roofs, and countless technical applications.
Summary
The right circular cone stands as a symbol of the perfection of rotational geometry and the elegance of mathematical relationships. Its simple creation through triangle rotation leads to a wealth of fascinating properties, from the fundamental volume and surface formulas to the classical conic sections. In practice, the cone finds countless applications, from architectural masterpieces to everyday objects. As a bridge between pure mathematics and applied geometry, the cone remains a fascinating example of the beauty and utility of geometric forms. Its universality and mathematical elegance make it one of the most important rotational solids in geometry, demonstrating how simple principles can create forms of enduring beauty and practical value.