Pyramid Frustum Calculator
Calculator and formulas for calculating a regular pyramid frustum
Pyramid Frustum Calculator
The Regular Pyramid Frustum
A regular pyramid frustum is a truncated pyramid with parallel top and bottom faces.
Regular Pyramid Frustum Properties
The truncated pyramid: Cut parallel to the base at a specific height
Pyramid Frustum Structure
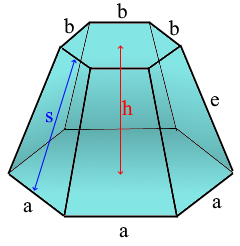
A regular pyramid frustum with parallel faces.
Truncated pyramid structure.
|
|
What is a Regular Pyramid Frustum?
A regular pyramid frustum is a fascinating truncated polyhedron:
- Definition: A pyramid with the top cut off parallel to the base
- Structure: Two parallel polygon faces connected by trapezoids
- Regular: Both bases are regular polygons
- Faces: 2 polygon bases + n trapezoidal faces
- Stability: Excellent structural properties
- Versatility: Common in engineering applications
Geometric Properties of Pyramid Frustums
The regular pyramid frustum exhibits unique geometric properties:
Basic Elements
- Bottom base: Regular polygon with side length a
- Top base: Similar polygon with side length b
- Height: Perpendicular distance between bases
- Slant height: Distance along trapezoidal face
Special Properties
- Parallel bases: Top and bottom faces are parallel
- Similar: Both bases are similar polygons
- Trapezoidal faces: n congruent trapezoids
- Convex: All faces point outward
Mathematical Relationships
The regular pyramid frustum follows sophisticated mathematical laws:
Volume Formula
Involves both base areas and their geometric mean. Advanced truncation formula.
Surface Area Formula
Sum of both bases plus lateral surface. Trapezoidal face calculations.
Applications of Pyramid Frustums
Regular pyramid frustums are essential in many engineering fields:
Architecture & Construction
- Building foundations and footings
- Stepped pyramid structures
- Decorative architectural elements
- Structural transition pieces
Engineering & Manufacturing
- Container and tank designs
- Hopper and funnel structures
- Pipe transition sections
- Machine component housings
Civil Engineering
- Dam and spillway structures
- Retaining wall designs
- Bridge pier foundations
- Canal and channel transitions
Education & Research
- Geometry education models
- 3D visualization tools
- Mathematical demonstrations
- Engineering design studies
Regular Pyramid Frustum Formulas
Slant height (\(\small{s}\))
Distance along the trapezoidal face
Edge length (\(\small{e}\))
Length of the lateral edges
Base and top area (\(\small{A}\))
Combined area of both polygon bases
Slant area (\(\small{A_s}\))
Area of one trapezoidal face
Lateral surface (\(\small{A_L}\))
Total area of all trapezoidal faces
Surface area (\(\small{S}\))
Total surface area (bases + lateral)
Perimeter (\(\small{P}\))
Perimeter of the base polygon
Volume (\(\small{V}\))
Volume of the truncated pyramid
Calculation Example for a Pentagonal Pyramid Frustum
Given
Find: All properties of the pentagonal pyramid frustum
1. Slant Height Calculation
For a = 8, b = 5, h = 6, n = 5:
\[s = \sqrt{\frac{1}{4} \cdot \cot^2\left(\frac{\pi}{5}\right) \cdot (8-5)^2 + 6^2}\] \[s = \sqrt{\frac{1}{4} \cdot 2.377^2 \cdot 9 + 36}\] \[s = \sqrt{12.78 + 36} ≈ 6.98\]The slant height is approximately 6.98 units
2. Base Areas Calculation
For pentagon bases:
\[A = 5 \cdot \frac{8^2 + 5^2}{4 \cdot \tan\left(\frac{\pi}{5}\right)}\] \[A = 5 \cdot \frac{64 + 25}{4 \cdot 0.727}\] \[A = 5 \cdot \frac{89}{2.908} ≈ 153.01\]Combined base areas: ≈153.01 square units
3. Lateral Surface Calculation
For n = 5, s ≈ 6.98:
\[A_L = 5 \cdot \frac{(8 + 5) \cdot 6.98}{2}\] \[A_L = 5 \cdot \frac{13 \cdot 6.98}{2}\] \[A_L = 5 \cdot 45.37 = 226.85\]Lateral surface area: ≈226.85 square units
4. Volume Calculation
Using the frustum volume formula:
\[V = \frac{6}{3} \cdot \left(153.01 + \sqrt{\frac{5^2 \cdot 8^2 \cdot 5^2}{2.908^2}}\right)\] \[V ≈ 2 \cdot (153.01 + 137.41) ≈ 580.84\]Volume: ≈580.84 cubic units
5. Complete Pentagonal Pyramid Frustum Summary
The pentagonal pyramid frustum with perfect engineering proportions
The Regular Pyramid Frustum: Engineering Versatility in Geometry
The regular pyramid frustum represents one of the most practical and versatile geometric forms in engineering and architecture. Created by cutting a pyramid parallel to its base, this truncated structure combines the stability of a wide foundation with the efficiency of a tapered design. The mathematical complexity of frustum calculations reflects the sophisticated relationships between the two parallel polygon bases and their connecting trapezoidal faces, making it an essential tool for engineers, architects, and designers working with transitional structures.
The Geometry of Practical Design
The regular pyramid frustum demonstrates the power of geometric optimization:
- Structural Efficiency: Optimal material distribution from large to small cross-sections
- Load Distribution: Superior weight transfer from top to bottom
- Space Utilization: Maximizes volume while minimizing material usage
- Flow Dynamics: Excellent for directing flows and transitions
- Stability: Wide base provides excellent foundational support
- Scalability: Properties scale predictably with dimensional changes
- Modularity: Can be stacked or combined for complex structures
Mathematical Sophistication
Advanced Relationships
The formulas for pyramid frustums involve complex trigonometric relationships and square roots, combining polygon geometry with three-dimensional truncation principles to create precise engineering calculations.
Geometric Integration
The volume formula elegantly integrates the areas of both bases with their geometric mean, reflecting the smooth transition between different cross-sectional sizes.
Engineering Applications
From foundation design to industrial hoppers, pyramid frustums serve critical structural and functional roles where gradual transitions and stable bases are essential.
Design Flexibility
The ability to vary both base dimensions and height independently allows designers to optimize frustums for specific structural, aesthetic, and functional requirements.
Summary
The regular pyramid frustum stands as a testament to the practical application of advanced geometry in modern engineering. Its complex mathematical relationships, involving cotangent functions, geometric means, and polynomial expressions, describe a form that serves essential functions across numerous industries. From the foundations of skyscrapers to the hoppers of industrial facilities, pyramid frustums demonstrate how sophisticated mathematical precision enables structures that are both efficient and beautiful. The truncated pyramid continues to prove its worth as engineers and architects seek solutions that optimize material usage, structural integrity, and functional performance. Its enduring relevance in contemporary design reflects the timeless value of geometric wisdom applied to practical challenges.