Hexagonal Bipyramid Calculator
Calculator and formulas for calculating a regular hexagonal bipyramid (or dipyramid)
Hexagonal Bipyramid Calculator
The Hexagonal Bipyramid
This function calculates the properties of a regular hexagonal bipyramid. The hexagonal bipyramid consists of 12 triangular faces forming a double pyramid with six-fold symmetry. Enter the base side length and height.
Hexagonal Bipyramid Properties
The double hexagonal pyramid: 12 triangular faces forming perfect six-fold symmetry
Hexagonal Bipyramid Structure
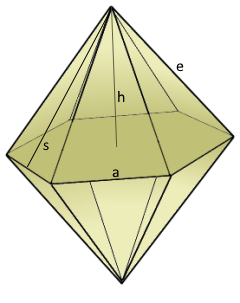
The regular hexagonal bipyramid with 12 triangular faces.
Perfect six-fold rotational symmetry.
|
|
What is a Hexagonal Bipyramid?
The hexagonal bipyramid is a fascinating double pyramid structure:
- Definition: Two hexagonal pyramids joined at their bases
- Structure: 12 congruent triangular faces forming a closed polyhedron
- No base: Unlike single pyramids, bipyramids have no flat base surface
- Vertices: 8 vertices (6 equatorial + 2 polar)
- Edges: 18 edges (6 equatorial + 12 connecting)
- Symmetry: Perfect 6-fold rotational symmetry
Geometric Properties of the Hexagonal Bipyramid
The hexagonal bipyramid shows remarkable six-fold geometric properties:
Basic Parameters
- Faces: 12 triangular faces (no base)
- Vertices: 8 vertices (6 equatorial + 2 polar)
- Edges: 18 edges (6 + 12)
- Euler Characteristic: V - E + F = 8 - 18 + 12 = 2
Special Properties
- Double Structure: Two pyramids fused together
- Six-fold Symmetry: Perfect hexagonal symmetry
- Deltahedron: All faces are triangles
- Equatorial Plane: Hexagonal cross-section at center
Mathematical Relationships
The hexagonal bipyramid follows elegant hexagonal geometry laws:
Volume Formula
Special hexagonal relationship. Uses tan(30°) = √3/3.
Surface Area Formula
Twelve triangular faces. No base area to add.
Applications of the Hexagonal Bipyramid
Hexagonal bipyramids find specialized applications:
Science & Crystallography
- Crystal structures and mineralogy
- Molecular geometry studies
- Quasicrystal patterns
- Materials science applications
Architecture & Design
- Modern geometric structures
- Decorative architectural elements
- Space frame constructions
- Geodesic dome components
Education & Learning
- Advanced 3D geometry studies
- Polyhedra classification
- Symmetry group theory
- Mathematical modeling
Art & Manufacturing
- Geometric sculptures and art
- 3D printing applications
- Jewelry and ornament design
- Industrial component shapes
Hexagonal Bipyramid Formulas
Slant Height (s)
Slant height with cotangent relationship for hexagon
Edge Length (e)
Special edge length formula for bipyramid
Total Height (i)
Total height from apex to apex
Slant Area (As)
Area of one triangular face
Surface Area (S)
Total area of all 12 triangular faces
Perimeter (P)
Perimeter of the hexagonal equatorial cross-section
Volume (V)
Volume using hexagonal base area and height, simplified with √3
Calculation Example for a Hexagonal Bipyramid
Given
Find: All properties of the regular hexagonal bipyramid
1. Slant Height Calculation
For hexagon (n=6), a=6, h=12:
\[s = \sqrt{h^2 + \frac{a^2 \cdot \cot^2(\frac{\pi}{6})}{4}}\] \[= \sqrt{12^2 + \frac{6^2 \cdot \cot^2(30°)}{4}}\] \[= \sqrt{144 + \frac{36 \cdot (\sqrt{3})^2}{4}}\] \[= \sqrt{144 + \frac{36 \cdot 3}{4}} = \sqrt{144 + 27} = \sqrt{171} ≈ 13.08\]The slant height is approximately 13.08 units
2. Edge Length Calculation
Edge length for bipyramid:
\[e = \sqrt{\frac{s^2 + a^2}{4}}\] \[= \sqrt{\frac{13.08^2 + 6^2}{4}}\] \[= \sqrt{\frac{171.09 + 36}{4}}\] \[= \sqrt{\frac{207.09}{4}} = \sqrt{51.77} ≈ 7.19\]The edge length is approximately 7.19 units
3. Total Height Calculation
Total height from apex to apex:
\[i = 2 \cdot h = 2 \cdot 12 = 24\]Perimeter of hexagonal cross-section:
\[P = 6 \cdot a = 6 \cdot 6 = 36\]Total height: 24 units, Perimeter: 36 units
4. Surface Area Calculations
Triangular face areas:
Slant Area: \(A_s = \frac{a \cdot s}{2} = \frac{6 \cdot 13.08}{2} ≈ 39.24\)Surface Area: \(S = 6 \cdot a \cdot s = 6 \cdot 6 \cdot 13.08 ≈ 470.88\)
(Alternative: S = 12 × As = 12 × 39.24 ≈ 470.88)
One triangle area: 39.24, Total surface: 470.88
5. Volume Calculation
Volume using hexagonal formula:
\[V = \frac{a^2 \cdot h}{\tan(\frac{\pi}{6})}\] \[= \frac{6^2 \cdot 12}{\tan(30°)}\] \[= \frac{36 \cdot 12}{\frac{\sqrt{3}}{3}} = \frac{432 \cdot 3}{\sqrt{3}}\] \[= \frac{1296}{\sqrt{3}} = 432\sqrt{3} ≈ 748.28\]The volume is approximately 748.28 cubic units
6. The Perfect Hexagonal Bipyramid
The regular hexagonal bipyramid with perfect six-fold symmetry
The Hexagonal Bipyramid: Double pyramid perfection
The hexagonal bipyramid is a remarkable geometric form that exemplifies the beauty of double pyramid structures. By joining two hexagonal pyramids at their bases, this polyhedron creates a perfectly symmetrical shape with 12 triangular faces and no flat surfaces. The six-fold rotational symmetry of the hexagon creates unique mathematical relationships involving the square root of 3 and special trigonometric values. This form appears naturally in crystal structures, molecular geometry, and modern architectural designs where both structural strength and aesthetic appeal are paramount. The hexagonal bipyramid represents an optimal balance between geometric complexity and mathematical elegance.
The Geometry of Six-fold Double Symmetry
The hexagonal bipyramid shows the ultimate in double pyramid symmetry:
- Hexagonal Foundation: Based on the regular hexagon with its perfect 120° angles
- Double Structure: Two pyramid halves creating perfect bilateral symmetry
- Six-fold Rotation: Perfect symmetry at 60° intervals around the central axis
- Twelve Triangles: All faces are congruent isosceles triangles
- No Base Surface: Completely enclosed with only triangular faces
- Equatorial Plane: Hexagonal cross-section at the widest point
- Crystallographic Form: Common in natural crystal formations
Mathematical Sophistication
Hexagonal Trigonometry
The volume formula V = a²h/tan(π/6) simplifies to V = a²h√3, showcasing the fundamental role of √3 in hexagonal geometry and the 30°-60°-90° triangle relationships.
Double Pyramid Symmetry
The bipyramid structure creates perfect symmetry across the equatorial plane, with each half being a mirror image of the other, resulting in unique geometric properties.
Crystallographic Applications
Many crystal systems exhibit hexagonal bipyramid structures, making this form essential in mineralogy, materials science, and crystal engineering applications.
Structural Efficiency
The combination of hexagonal base strength and double pyramid stability creates an exceptionally strong and efficient geometric form for engineering applications.
Summary
The hexagonal bipyramid represents the pinnacle of double pyramid geometry, combining the strength and beauty of hexagonal symmetry with the elegance of bipyramidal structure. Its twelve triangular faces create a closed polyhedron that embodies both mathematical sophistication and practical utility. The special trigonometric relationships involving √3 and the 30° angle make it a favorite subject for advanced geometry studies. From crystal formations in nature to cutting-edge architectural designs, the hexagonal bipyramid demonstrates how geometric perfection can emerge from the fusion of simple forms. Its applications span from the microscopic world of molecular structures to the macroscopic realm of modern architecture, proving that mathematical beauty and practical functionality can coexist in perfect harmony. The hexagonal bipyramid stands as a testament to the power of geometric symmetry and the endless possibilities that arise when mathematical principles guide structural design.