Triangular Bipyramid Calculator
Calculator and formulas for the triangular bipyramid (dipyramid) - Johnson solid J12
Triangular Bipyramid Calculator
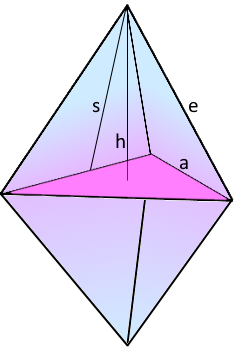
The Triangular Bipyramid (J12)
The triangular bipyramid is a Johnson solid (J12) consisting of 6 equilateral triangles - two tetrahedra joined at their bases.
Johnson Solid J12 Properties
The double tetrahedron: Two tetrahedra joined at their triangular bases
Triangular Bipyramid Structure
The double tetrahedron with perfect symmetry.
Johnson solid J12 - 6 equilateral triangles.
|
|
What is a triangular bipyramid?
The triangular bipyramid is a fascinating Johnson solid and geometric masterpiece:
- Definition: Two tetrahedra joined at their triangular bases
- Johnson solid: J12 in the classification system
- Faces: 6 congruent equilateral triangles
- Vertices: 6 vertices (4 equatorial, 2 polar)
- Edges: 9 edges (all equal length)
- Symmetry: Perfect D3h symmetry
Geometric Properties of the Triangular Bipyramid
The triangular bipyramid shows remarkable geometric properties:
Basic Parameters
- Faces: 6 equilateral triangles
- Vertices: 6 vertices (4 equatorial, 2 polar)
- Edges: 9 edges (all equal length)
- Euler characteristic: V - E + F = 6 - 9 + 6 = 3? No! = 2
Special Properties
- Deltahedron: All faces are triangles
- Equilateral: All triangles are equilateral
- Double-tetrahedron: Two tetrahedra connected
- Convex: No concave edges or vertices
Mathematical Relationships
The triangular bipyramid follows simple but elegant laws:
Volume Formula
Uses triangular geometry. Contains √3 relationships.
Surface Formula
Six identical equilateral triangles. Simple multiplication formula.
Applications of the Triangular Bipyramid
Triangular bipyramids find applications in various fields:
Architecture & Construction
- Pyramidal roof constructions
- Decorative spires and finials
- Structural supports and braces
- Garden and landscape sculptures
Science & Technology
- Crystallographic structures
- Molecular geometry models
- Optical prisms and lenses
- Antenna design elements
Education & Teaching
- Geometry instruction models
- 3D geometry demonstrations
- Johnson solid studies
- Symmetry and group theory
Art & Design
- Geometric sculptures and installations
- Modern art and architecture
- Jewelry and decorative objects
- 3D printed artistic creations
Triangular Bipyramid Formulas
Volume (V)
Volume using triangular base area and height
Surface Area (S)
Six equilateral triangles (alternative: 6 × triangle area)
Slant Height (s)
From center of triangular base to apex
Edge Length (e)
Length of edges from base vertices to apex
Total Height (i)
Full height from apex to apex
Slant Area (As)
Area of one triangular face
Johnson Solid J12 Properties
6 equilateral △
6 vertices
9 edges
D3h
Perfect geometric properties following from the double tetrahedron structure
Calculation Example for a Triangular Bipyramid
Given - Double Tetrahedron
Find: All properties of the triangular bipyramid (double tetrahedron)
1. Volume Calculation
Using the volume formula:
\[V = \frac{6^2 \cdot 4}{2\sqrt{3}} = \frac{36 \cdot 4}{2\sqrt{3}}\] \[V = \frac{144}{2 \cdot 1.732} = \frac{144}{3.464}\] \[V ≈ 41.57\]The volume is approximately 41.57 cubic units
2. Surface Area Calculation
Six equilateral triangles:
\[S = \frac{3\sqrt{3}}{2} \cdot 6^2 = \frac{3\sqrt{3}}{2} \cdot 36\] \[S = \frac{108\sqrt{3}}{2} = 54\sqrt{3}\] \[S ≈ 54 \times 1.732 ≈ 93.53\]The surface area is approximately 93.53 square units
3. Slant Height Calculation
Slant height to face center:
\[s = \sqrt{4^2 + \frac{6^2 \cdot \cot^2(60°)}{4}}\] \[s = \sqrt{16 + \frac{36 \cdot (1/\sqrt{3})^2}{4}}\] \[s = \sqrt{16 + 3} = \sqrt{19} ≈ 4.36\]The slant height is approximately 4.36 units
4. Additional Properties
Other measurements:
\[\text{Total height: } i = 2 \times 4 = 8\] \[\text{Perimeter: } P = 3 \times 6 = 18\] \[\text{Slant area: } A_s = \frac{6 \times 4.36}{2} ≈ 13.08\]Complete geometric characterization
Complete Double Tetrahedron Results
Perfect triangular bipyramid - the elegant double tetrahedron
The Triangular Bipyramid: The Double Tetrahedron Masterpiece
The triangular bipyramid, also known as the double tetrahedron, represents one of the most elegant and fundamental shapes in three-dimensional geometry. As Johnson solid J12, this remarkable polyhedron consists of exactly six equilateral triangles arranged with perfect D3h symmetry, creating a form that embodies both mathematical beauty and structural perfection. The bipyramid emerges from the union of two tetrahedra joined at their triangular bases, creating a shape that maintains all the geometric purity of its constituent parts while achieving a higher level of symmetric complexity that has fascinated mathematicians and designers for centuries.
The Geometry of Perfect Symmetry
The triangular bipyramid showcases the pinnacle of geometric elegance:
- Double tetrahedron: Two perfect tetrahedra united at their bases
- Deltahedron: All six faces are congruent equilateral triangles
- D3h symmetry: Three-fold rotational symmetry with mirror planes
- Johnson solid: J12 in the comprehensive classification
- Uniform edges: All nine edges have identical length
- Polar symmetry: Two apices with four equatorial vertices
- Convex perfection: No concave surfaces or irregular features
Mathematical Elegance and Relationships
Triangular Foundation
The volume formula elegantly incorporates the triangular geometry through the √3 factor, reflecting the equilateral triangle's fundamental mathematical relationships and area calculations.
Symmetric Perfection
The surface area formula demonstrates the beautiful simplicity of six identical triangular faces, each contributing equally to the total surface in perfect geometric harmony.
Pythagorean Integration
The slant height calculation seamlessly combines the Pythagorean theorem with trigonometric relationships, creating robust geometric connections throughout the structure.
Tetrahedral Heritage
As a double tetrahedron, it inherits the structural strength and geometric purity of the tetrahedron while creating new symmetries and applications through its bipyramidal form.
Summary
The triangular bipyramid stands as a masterpiece of geometric perfection, embodying the elegant simplicity that emerges when fundamental shapes are combined with mathematical precision. Its six equilateral triangular faces, arranged in perfect D3h symmetry, create a form that is simultaneously simple and sophisticated, familiar yet extraordinary. The mathematical relationships governing this double tetrahedron—involving √3 factors, trigonometric functions, and Pythagorean principles—demonstrate how geometric beauty naturally emerges from mathematical truth. Whether serving as a structural element in architecture, a model in crystallography, or an object of pure mathematical study, the triangular bipyramid continues to inspire with its perfect balance of symmetry, strength, and elegance. Understanding its properties provides insight into fundamental geometric principles while revealing the inherent beauty that lies at the intersection of mathematics and three-dimensional form.