Bipyramid Calculator
Calculator and formulas for calculating a regular bipyramid (or dipyramid)
Bipyramid Calculator
The Regular Bipyramid
A regular bipyramid is a double pyramid with identical pyramids joined at their bases.
Regular Bipyramid Properties
The double pyramid: Two identical pyramids joined at their bases
Bipyramid Structure
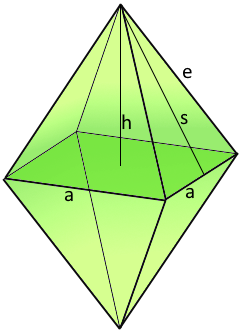
A regular bipyramid with perfect symmetry.
Double pyramid structure.
|
|
What is a Regular Bipyramid?
A regular bipyramid (or dipyramid) is a fascinating polyhedron:
- Definition: Two congruent pyramids joined base-to-base
- Structure: Symmetrical double pyramid
- Faces: 2n congruent triangular faces
- Vertices: n+2 vertices total
- Edges: 3n edges
- Symmetry: Perfect rotational symmetry
Geometric Properties of Bipyramids
The regular bipyramid exhibits remarkable geometric properties:
Basic Parameters
- Faces: 2n congruent triangular faces
- Vertices: n+2 vertices (n equatorial, 2 polar)
- Edges: 3n edges total
- Euler characteristic: V - E + F = 2
Special Properties
- Symmetric: Perfect mirror symmetry
- Regular: All faces are congruent
- Convex: All vertices point outward
- Dual: Self-dual for certain cases
Mathematical Relationships
The regular bipyramid follows elegant mathematical laws:
Volume Formula
Contains cotangent functions for base polygons. Elegant and precise.
Surface Area Formula
Based on triangular faces. Simple multiplication by n.
Applications of Bipyramids
Regular bipyramids find applications in various fields:
Architecture & Construction
- Pyramidal roof structures
- Decorative spires and finials
- Structural framework elements
- Sculptural architectural features
Science & Technology
- Crystallographic structures
- Molecular geometry models
- Optical prism designs
- Mechanical components
Education & Teaching
- Geometry instruction
- 3D spatial reasoning
- Polyhedron classification
- Mathematical modeling
Art & Design
- Geometric sculptures
- Modern art installations
- Decorative objects
- Jewelry design
Bipyramid Formulas
Slant height (\(\small{s}\))
Distance from apex to base edge midpoint
Edge length (\(\small{e}\))
Length of triangular face edges
Total height (\(\small{i}\))
Total height of the bipyramid
Slant area (\(\small{A_s}\))
Area of one triangular face
Surface area (\(\small{S}\))
Total surface area of all faces
Perimeter (\(\small{P}\))
Perimeter of the base polygon
Volume (\(\small{V}\))
Total volume of the bipyramid (both pyramid halves)
Calculation Example for a Square Bipyramid
Given
Find: All properties of the square bipyramid
1. Slant Height Calculation
For a = 8, h = 10, n = 4:
\[s = \sqrt{10^2 + \frac{8^2 \cdot \cot^2(\frac{\pi}{4})}{4}}\] \[s = \sqrt{100 + \frac{64 \cdot 1^2}{4}}\] \[s = \sqrt{100 + 16} = \sqrt{116} ≈ 10.77\]The slant height is approximately 10.77 units
2. Surface Area Calculation
For n = 4, a = 8, s ≈ 10.77:
\[S = n \cdot a \cdot s\] \[S = 4 \cdot 8 \cdot 10.77\] \[S ≈ 344.64\]The surface area is approximately 344.64 square units
3. Volume Calculation
For n = 4, a = 8, h = 10:
\[V = \frac{2 \cdot 4 \cdot 8^2 \cdot 10}{12 \cdot \tan(\frac{\pi}{4})}\] \[V = \frac{5120}{12 \cdot 1} = \frac{5120}{12} ≈ 426.67\]The volume is approximately 426.67 cubic units
4. The Perfect Square Bipyramid
The square bipyramid with perfect double pyramid symmetry
The Regular Bipyramid: A Study in Perfect Symmetry
The regular bipyramid represents one of geometry's most elegant examples of perfect symmetry and mathematical beauty. By joining two congruent pyramids base-to-base, we create a structure that embodies the principles of balance, proportion, and geometric harmony. The mathematical relationships governing bipyramids involve trigonometric functions and square roots, creating formulas that are both complex enough to be interesting and simple enough to be practical for real-world applications.
The Geometry of Double Pyramids
The regular bipyramid demonstrates the beauty of geometric symmetry:
- Perfect Symmetry: Mirror symmetry about the central plane
- Rotational Symmetry: n-fold rotational symmetry around the central axis
- Uniform Structure: All triangular faces are congruent
- Convex Form: All vertices point outward from the center
- Stable Base: The equatorial polygon provides structural stability
- Scalability: Properties scale predictably with size
- Versatility: Can be constructed with any regular polygon base
Mathematical Elegance
Trigonometric Beauty
The formulas for bipyramids showcase the elegant interplay between trigonometry and geometry, with cotangent and tangent functions naturally arising from the polygon-pyramid relationship.
Structural Harmony
The bipyramid's proportions create natural relationships between linear, area, and volume measurements, making it ideal for architectural and engineering applications.
Practical Applications
From crystallography to architecture, bipyramids appear in nature and human design as efficient, stable, and aesthetically pleasing structures.
Educational Value
The bipyramid serves as an excellent teaching tool for 3D geometry, combining basic concepts with more advanced mathematical relationships.
Summary
The regular bipyramid stands as a testament to the power of geometric symmetry and mathematical precision. Its elegant structure, described by formulas involving trigonometric functions and square roots, makes it both mathematically interesting and practically useful. From the pyramids of ancient Egypt to modern architectural marvels, the bipyramid continues to inspire mathematicians, architects, and designers. Whether studied for its pure geometric beauty or applied in practical construction, the bipyramid remains one of the most perfect examples of how mathematical principles can create structures of lasting beauty and utility.