Heptagonal Pyramid Calculator
Calculator and formulas for calculating a regular heptagonal pyramid
Heptagonal Pyramid Calculator
The Heptagonal Pyramid
This function calculates the properties of a regular heptagonal pyramid. The heptagonal pyramid has a regular heptagon (7-sided polygon) as its base. Enter the base side length and height to calculate all properties.
Heptagonal Pyramid Properties
The seven-sided pyramid: Regular heptagon base with 7 triangular faces
Heptagonal Pyramid Structure
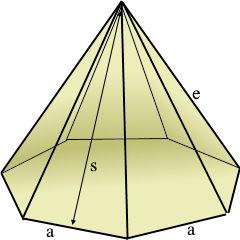
The regular heptagonal pyramid with 7-sided base.
Perfect seven-fold rotational symmetry.
|
|
What is a Heptagonal Pyramid?
The heptagonal pyramid is a fascinating seven-sided geometric form:
- Definition: Pyramid with a regular heptagon (7-sided polygon) as base
- Base: Regular heptagon with 7 equal sides and angles
- Faces: 1 regular heptagon + 7 congruent triangular faces
- Vertices: 8 vertices (7 base + 1 apex)
- Edges: 14 edges (7 base + 7 lateral)
- Symmetry: 7-fold rotational symmetry
Geometric Properties of the Heptagonal Pyramid
The heptagonal pyramid shows unique seven-sided geometric properties:
Basic Parameters
- Faces: 8 (1 heptagon + 7 triangles)
- Vertices: 8 (7 base + 1 apex)
- Edges: 14 (7 base + 7 lateral)
- Euler Characteristic: V - E + F = 8 - 14 + 8 = 2
Special Properties
- Seven-fold Symmetry: 7-fold rotational symmetry
- Regular Base: All 7 base sides are equal
- Congruent Faces: All 7 side faces are identical
- Prime Number: Based on prime number 7
Mathematical Relationships
The heptagonal pyramid follows elegant trigonometric laws:
Volume Formula
Base area with tangent relationship. Seven-fold trigonometry.
Base Area Formula
Heptagon area with tangent. Seven-sided perfection.
Applications of the Heptagonal Pyramid
Heptagonal pyramids find specialized applications:
Architecture & Construction
- Specialized roof designs
- Unique tower tops
- Modern geometric buildings
- Decorative architectural elements
Science & Technology
- Crystallographic structures
- Optical prism designs
- 7-fold symmetric systems
- 3D printing applications
Education & Learning
- Advanced trigonometry applications
- Heptagon geometry studies
- 3D geometry challenges
- Prime number geometry concepts
Art & Design
- Seven-fold symmetric sculptures
- Unique geometric artworks
- Specialized product design
- Mathematical art installations
Heptagonal Pyramid Formulas
Slant Height (s)
Slant height with cotangent relationship for heptagon
Edge Length (e)
Edge length from apex to base vertices
Base Area (A)
Area of the regular heptagon base
Slant Area (As)
Area of one triangular side face
Lateral Surface (AL)
Sum of all 7 triangular side faces
Surface Area (S)
Base area plus lateral surface area
Perimeter (P)
Perimeter of the heptagonal base
Volume (V)
One third base area times height
Calculation Example for a Heptagonal Pyramid
Given
Find: All properties of the regular heptagonal pyramid
1. Base Area Calculation
For n=7, a=8:
\[A = \frac{7 \cdot a^2}{4 \cdot \tan(\frac{\pi}{7})}\] \[= \frac{7 \cdot 8^2}{4 \cdot \tan(\frac{\pi}{7})}\] \[= \frac{7 \cdot 64}{4 \cdot \tan(25.71°)}\] \[= \frac{448}{4 \cdot 0.4816} ≈ \frac{448}{1.926} ≈ 232.61\]The base area is approximately 232.61 square units
2. Slant Height Calculation
Slant height for n=7:
\[s = \sqrt{h^2 + \frac{a^2 \cdot \cot^2(\frac{\pi}{7})}{4}}\] \[= \sqrt{10^2 + \frac{8^2 \cdot \cot^2(25.71°)}{4}}\] \[= \sqrt{100 + \frac{64 \cdot 2.077^2}{4}}\] \[= \sqrt{100 + \frac{64 \cdot 4.314}{4}} ≈ \sqrt{100 + 69.02} ≈ 13.01\]The slant height is approximately 13.01 units
3. Edge Length Calculation
Edge length from apex to vertices:
\[e = \sqrt{s^2 + \frac{a^2}{4}}\] \[= \sqrt{13.01^2 + \frac{8^2}{4}}\] \[= \sqrt{169.26 + \frac{64}{4}}\] \[= \sqrt{169.26 + 16} = \sqrt{185.26} ≈ 13.61\]The edge length is approximately 13.61 units
4. Surface Area Calculations
Side and lateral surface areas:
Slant Area: \(A_s = \frac{a \cdot s}{2} = \frac{8 \cdot 13.01}{2} ≈ 52.04\)Lateral Surface: \(A_L = 7 \cdot A_s = 7 \cdot 52.04 ≈ 364.28\)
Surface Area: \(S = A + A_L = 232.61 + 364.28 ≈ 596.89\)
Slant area: 52.04, Lateral surface: 364.28, Surface area: 596.89
5. Volume and Perimeter
Volume and base perimeter:
Volume: \(V = \frac{A \cdot h}{3} = \frac{232.61 \cdot 10}{3} ≈ 775.37\)Perimeter: \(P = 7 \cdot a = 7 \cdot 8 = 56\)
Volume: 775.37, Perimeter: 56 units
6. The Perfect Heptagonal Pyramid
The regular heptagonal pyramid with perfect seven-fold symmetry
The Heptagonal Pyramid: Seven-fold geometric perfection
The heptagonal pyramid is a remarkable seven-sided geometric form that combines the mathematical beauty of the regular heptagon with the structural elegance of the pyramid. As one of the less common pyramid forms, it showcases the unique properties that emerge when the number 7 - a prime number - becomes the foundation of geometric construction. The heptagonal pyramid demonstrates advanced trigonometric relationships and represents a perfect example of how prime numbers create distinctive geometric patterns. This form is particularly interesting in crystallography, architecture, and mathematical art where seven-fold symmetry creates visually striking and structurally unique results.
The Geometry of Seven-fold Symmetry
The heptagonal pyramid shows the unique properties of seven-fold symmetry:
- Prime Base: Seven-sided regular heptagon based on prime number geometry
- Seven-fold Rotation: Perfect rotational symmetry at 360°/7 ≈ 51.43° intervals
- Unique Trigonometry: Special trigonometric values for π/7 angles
- Congruent Triangles: Seven identical triangular faces meeting at the apex
- Prime Number Properties: Geometric characteristics unique to prime-based polygons
- Advanced Mathematics: Requires sophisticated trigonometric calculations
- Structural Uniqueness: Distinctive appearance due to seven-fold symmetry
Mathematical Sophistication
Prime Number Geometry
The base area formula A = 7a²/(4tan(π/7)) involves the special trigonometric value tan(π/7), which cannot be expressed in simple radical form and requires advanced mathematical techniques.
Seven-fold Trigonometry
The angles and relationships in a heptagon involve the seventh roots of unity and complex trigonometric identities, making this pyramid mathematically sophisticated.
Crystallographic Applications
Seven-fold symmetry appears in certain crystal structures and quasicrystals, making the heptagonal pyramid relevant in materials science and crystallography.
Artistic Uniqueness
The distinctive seven-fold symmetry creates visually striking patterns that are neither too simple nor too complex, making it popular in architectural and artistic applications.
Summary
The heptagonal pyramid represents a fascinating intersection of prime number theory, advanced trigonometry, and geometric beauty. Its seven-fold symmetry creates a unique visual and mathematical identity that sets it apart from more common pyramid forms. The mathematical relationships involved, particularly the trigonometric functions of π/7, showcase some of the most sophisticated aspects of geometric calculation. From crystallographic structures to architectural elements, the heptagonal pyramid demonstrates how prime numbers create distinctive geometric patterns. Its applications in science, technology, and art highlight the continuing relevance of advanced geometric forms. The heptagonal pyramid is not just a mathematical curiosity, but a practical form that bridges the gap between pure mathematics and applied geometry, showing how the number seven creates unique structural and aesthetic possibilities that cannot be achieved with other polygon-based pyramids.