Triangular Pyramid Calculator
Calculator and formulas for the regular triangular pyramid (tetrahedron) - the fundamental 3D shape
Tetrahedron Calculator
The Regular Triangular Pyramid
The regular triangular pyramid is the tetrahedron - the most fundamental 3D shape with 4 equilateral triangular faces.
Tetrahedron Properties
The fundamental solid: The simplest 3D shape with minimum vertices, edges, and faces
Tetrahedron Structure
The fundamental tetrahedron - simplest 3D shape.
Platonic solid with perfect triangular faces.
|
|
What is a regular triangular pyramid?
The regular triangular pyramid (tetrahedron) is the most fundamental 3D geometric shape:
- Definition: A pyramid with an equilateral triangular base
- Tetrahedron: The simplest 3D polyhedron possible
- Faces: 4 congruent equilateral triangles
- Vertices: 4 vertices (minimum for 3D shape)
- Edges: 6 edges (all equal length)
- Platonic solid: One of the five perfect solids
Geometric Properties of the Tetrahedron
The tetrahedron exhibits the most fundamental geometric properties:
Fundamental Parameters
- Faces: 4 equilateral triangles (minimum for 3D)
- Vertices: 4 vertices (minimum for 3D polyhedron)
- Edges: 6 edges (all equal length)
- Euler characteristic: V - E + F = 4 - 6 + 4 = 2
Special Properties
- Platonic solid: One of five perfect regular polyhedra
- Self-dual: Dual polyhedron is also a tetrahedron
- Maximum symmetry: Perfect tetrahedral symmetry
- Minimal complexity: Simplest possible 3D shape
Mathematical Relationships
The tetrahedron follows the most fundamental mathematical laws:
Volume Formula
Contains fundamental √3 relationships. Simplest 3D volume formula.
Surface Area Formula
Four identical equilateral triangles. Fundamental triangular geometry.
Applications of the Tetrahedron
Tetrahedra are fundamental across countless fields:
Architecture & Construction
- Structural framework systems
- Space frame construction
- Pyramidal architectural elements
- Geodesic dome components
Science & Technology
- Molecular geometry (methane, silicon)
- Crystal structures and lattices
- Finite element mesh generation
- 3D graphics and modeling
Education & Mathematics
- Introduction to 3D geometry
- Platonic solids education
- Coordinate geometry examples
- Volume and surface area calculations
Games & Entertainment
- 4-sided dice (D4) in gaming
- Puzzle and brain teaser designs
- 3D art and sculpture
- Virtual reality environments
Triangular Pyramid (Tetrahedron) Formulas
Volume (V)
Fundamental 3D volume formula with √3 factor
Base Area (A)
Area of equilateral triangular base
Surface Area (S)
Base area plus lateral area (3 triangular faces)
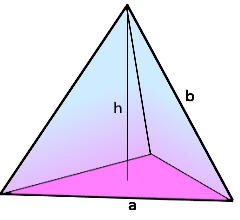
Edge Length (b)
Length of edges from base vertices to apex
Slant Height (s)
Height of triangular lateral faces
Slant Area (Am)
Total area of three lateral triangular faces
Tetrahedron Properties & Alternative Formulas
\(h = \frac{12V}{\sqrt{3} \cdot a^2}\)
All edges equal: \(a = b\)
Perfect symmetry
The tetrahedron is the foundation of all 3D geometry
Calculation Example for a Regular Triangular Pyramid
Given - Fundamental Tetrahedron
Find: All properties of the fundamental tetrahedron
1. Base Area Calculation
Equilateral triangle area:
\[A = \frac{\sqrt{3} \cdot 6^2}{4} = \frac{\sqrt{3} \cdot 36}{4}\] \[A = \frac{36\sqrt{3}}{4} = 9\sqrt{3}\] \[A ≈ 9 \times 1.732 ≈ 15.59\]The base area is approximately 15.59 square units
2. Volume Calculation
Tetrahedron volume:
\[V = \frac{\sqrt{3} \cdot 6^2 \cdot 8}{12} = \frac{\sqrt{3} \cdot 36 \cdot 8}{12}\] \[V = \frac{288\sqrt{3}}{12} = 24\sqrt{3}\] \[V ≈ 24 \times 1.732 ≈ 41.57\]The volume is approximately 41.57 cubic units
3. Edge Length Calculation
Lateral edge length:
\[b = \sqrt{8^2 + \frac{6^2}{3}} = \sqrt{64 + \frac{36}{3}}\] \[b = \sqrt{64 + 12} = \sqrt{76}\] \[b ≈ 8.72\]The lateral edge length is approximately 8.72 units
4. Surface Area Calculation
Slant height:
\[s = \sqrt{\frac{4 \cdot 76 - 36}{4}} = \sqrt{\frac{268}{4}} ≈ 8.19\]Total surface area:
\[S = 15.59 + \frac{3 \cdot 6 \cdot 8.19}{2} ≈ 89.30\]Total surface area is approximately 89.30 square units
Complete Tetrahedron Results
The fundamental tetrahedron - building block of all 3D geometry
The Tetrahedron: Foundation of All 3D Geometry
The regular triangular pyramid, universally known as the tetrahedron, stands as the most fundamental and essential shape in three-dimensional geometry. As the simplest possible polyhedron with the minimum number of vertices (4), edges (6), and faces (4) required to enclose three-dimensional space, the tetrahedron represents the very foundation upon which all other 3D geometry is built. This remarkable shape, one of the five Platonic solids, embodies perfect mathematical harmony through its four congruent equilateral triangular faces, each meeting three others at every vertex with identical angles and relationships that have fascinated mathematicians, scientists, and philosophers for over two millennia.
The Geometry of Fundamental Perfection
The tetrahedron showcases the absolute essence of 3D geometric perfection:
- Minimal complexity: The simplest possible 3D shape with maximum stability
- Platonic perfection: One of only five regular polyhedra possible in 3D space
- Self-dual nature: Its dual polyhedron is also a tetrahedron
- Tetrahedral symmetry: Highest possible symmetry for its vertex count
- Universal building block: Foundation for more complex geometric structures
- Mathematical elegance: All formulas involve fundamental constants like √3
- Structural perfection: Maximum strength with minimum material
Mathematical Significance and Universal Applications
Fundamental Mathematics
The tetrahedron's formulas represent the most basic relationships in 3D geometry, with √3 factors emerging naturally from triangular geometry and serving as building blocks for more complex calculations.
Scientific Foundation
From molecular structure (methane) to crystal lattices, the tetrahedral arrangement represents one of nature's most common and stable configurations.
Engineering Applications
The tetrahedron's inherent stability makes it fundamental in structural engineering, space frames, and finite element analysis where strength and simplicity are paramount.
Educational Importance
As the gateway to 3D understanding, the tetrahedron introduces students to volume, surface area, and spatial relationships in their most fundamental form.
Summary
The regular triangular pyramid—the tetrahedron—represents far more than just another geometric shape; it embodies the very essence of three-dimensional existence. Its perfect mathematical relationships, involving the fundamental √3 constant, demonstrate how geometric beauty emerges from mathematical necessity. As the simplest member of the Platonic solids, it connects us to ancient Greek mathematical tradition while remaining absolutely relevant in modern science, engineering, and technology. From the molecular structure of methane to the geodesic domes that grace our skylines, from the dice in our games to the finite elements in computer simulations, the tetrahedron's influence permeates every aspect of our three-dimensional world. Understanding its properties provides not just practical calculation skills, but insight into the fundamental principles that govern space, structure, and stability in our universe. The tetrahedron stands as proof that the most profound mathematical truths often reside in the simplest forms.