Oblique Cylinder Calculator
Calculator and formulas for calculating an oblique cylinder
Oblique Cylinder Calculator
The Oblique Cylinder
The oblique cylinder is an inclined circular cylinder with beveled end surfaces.
Oblique Cylinder Properties
The Oblique Cylinder: Inclined circular cylinder with beveled end surfaces
Oblique Cylinder Visualization
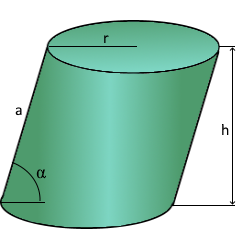
Oblique Cylinder
Inclined cylinder with angle α
Parameters
r: Radius of the base
α: Inclination angle
h: Vertical height
a: Side length (oblique)
Inclined circular cylinder.
Trigonometric relationships.
What is an Oblique Cylinder?
The oblique cylinder is an important geometric body:
- Definition: Circular cylinder with lateral surface inclined to the base
- Inclination angle α: Angle between side line and base
- Properties: Elliptical cross-sections with oblique cuts
- Distinction: Height h (vertical) vs. side length a (oblique)
- Applications: Architecture, mechanical engineering, oblique piping
- Mathematics: Trigonometric relationships h = a·sin(α)
Geometric Properties of the Oblique Cylinder
The oblique cylinder shows characteristic geometric properties:
Basic Parameters
- Radius r: Radius of the circular base
- Inclination angle α: Angle of the side line to the base
- Height h: Vertical distance between base surfaces
- Side length a: Oblique length of the generatrix
Special Properties
- Parallel sections: All parallel sections are congruent circles
- Oblique sections: Result in elliptical cross-sections
- Same volume: As vertical cylinder with same base and height
- Trigonometry: h = a·sin(α), a = h/sin(α)
Mathematical Relationships of the Oblique Cylinder
The oblique cylinder follows elegant trigonometric laws:
Volume Formula
The volume is identical to a vertical cylinder. Cavalieri's principle!
Trigonometric Relationship
Fundamental trigonometric relationship between height, side length, and inclination angle.
Applications of the Oblique Cylinder
Oblique cylinders find applications in various fields:
Architecture & Construction
- Oblique columns and supports
- Inclined pipelines
- Architectural elements
- Inclined elevators and ramps
Mechanical Engineering & Technology
- Oblique drilling
- Inclined cylinders in engines
- Hydraulic components
- Conveyor systems and chutes
Process Engineering
- Oblique reactors
- Inclined mixing vessels
- Filling devices
- Separation systems
Automotive Engineering
- Inclined engines (V-engines)
- Inclined exhaust pipes
- Hydraulic cylinders
- Suspension elements
Formulas for the Oblique Cylinder
Height (h)
Vertical height from side length and angle
Side Length (a)
Oblique side length from height and angle
Volume (V)
Volume same as vertical cylinder
Lateral Area (L)
Lateral surface with oblique side length
Additional Formulas
\[A = \pi r^2\]
\[P = 2\pi r\]
\[S = 2A + L\]
\[\cot(\alpha) = \frac{\sqrt{a^2-h^2}}{h}\]
The oblique cylinder connects geometry with trigonometry
Calculation Example for an Oblique Cylinder
Given
Find: All parameters of the oblique cylinder
1. Side Length Calculation
For h = 8 cm, α = 20°:
\[a = \frac{h}{\sin(\alpha)}\] \[a = \frac{8}{\sin(20°)}\] \[a = \frac{8}{0.342} ≈ 23.39 \text{ cm}\]The oblique side length is approximately 23.39 cm
2. Volume Calculation
For r = 3 cm, h = 8 cm:
\[V = \pi r^2 h\] \[V = \pi \cdot 3^2 \cdot 8\] \[V = \pi \cdot 9 \cdot 8 = 72\pi\] \[V ≈ 226.19 \text{ cm}^3\]The volume is approximately 226.19 cm³
3. Base Area and Perimeter
Base area and perimeter:
\[A = \pi r^2 = \pi \cdot 9 ≈ 28.27 \text{ cm}^2\] \[P = 2\pi r = 2\pi \cdot 3 = 6\pi ≈ 18.85 \text{ cm}\]Base area ≈ 28.27 cm², Perimeter ≈ 18.85 cm
4. Surface Area Calculation
Lateral area and total surface area:
\[L = 2\pi r a = 2\pi \cdot 3 \cdot 23.39\] \[L ≈ 441.07 \text{ cm}^2\] \[S = 2A + L = 2 \cdot 28.27 + 441.07\] \[S ≈ 497.61 \text{ cm}^2\]The total surface area is approximately 497.61 cm²
5. Trigonometric Verification
h = a·sin(α) = 23.39·sin(20°) ≈ 8.00 cm ✓
b = a·cos(20°) ≈ 21.97 cm
a² = h² + b² ✓
All trigonometric relationships are satisfied
6. Summary
The oblique cylinder with all characteristic parameters
7. Practical Example: Oblique Column
Inclined column
20° inclination
S ≈ 497.61 cm²
Surface area
Same volume
as vertical column
An oblique column offers architectural elegance with the same load-bearing capacity
8. Comparison with Vertical Cylinder
r=3, h=8, α=20°
V≈226.19 cm³
r=3, h=8
V≈226.19 cm³
Same volume!
Cavalieri's principle
The volume is identical with the same base area and height - a triumph of geometry!
The Oblique Cylinder: Trigonometry Meets Geometry
The oblique cylinder is a fascinating geometric body that combines the elegance of trigonometry with the practicality of cylinder geometry. As an inclined circular cylinder with beveled end surfaces, it retains all essential properties of the classic cylinder but extends them with the complexity of trigonometric relationships. This unique combination makes it an important element in architecture, mechanical engineering, and all areas where inclinations and oblique constructions play a role.
The Geometry of Inclination
The oblique cylinder shows the perfection of inclined geometry:
- Inclination angle α: Determines the oblique position of the lateral surface
- Height vs. side length: h = a·sin(α) - fundamental trigonometric relationship
- Same volume: Cavalieri's principle - identical to vertical cylinder
- Elliptical sections: Oblique cuts result in ellipses instead of circles
- Parallel sections: All sections parallel to the base remain circular
- Trigonometric elegance: Sine, cosine, and tangent in perfect harmony
- Practical versatility: Solutions for real construction problems
Versatile Applications
Architectural Innovation
Oblique columns and inclined supports create dynamic architecture and enable innovative structural solutions while maintaining stability.
Mechanical Engineering Precision
In technology, oblique cylinders enable optimized constructions for hydraulics, engine construction, and conveyor systems with exact trigonometric calculations.
Process Engineering Efficiency
Inclined reactors and mixing vessels utilize gravity optimally and improve mixing and process control through controlled inclination.
Automotive Engineering Perfection
V-engines and oblique cylinders maximize performance with minimal space requirements and show the practical elegance of inclined geometry.
Summary
The oblique cylinder embodies the perfect synthesis of trigonometric precision and geometric functionality. Its form, characterized by the inclination angle α and described by the elegant relationship h = a·sin(α), makes it one of the most versatile and practical geometric bodies. The fascinating Cavalieri principle shows that the volume remains identical to a vertical cylinder despite the inclination - a triumph of mathematical logic. From dynamic architectural elements to precise machine components to efficient process systems - the oblique cylinder proves that inclination means not complication, but innovation. It is living proof that trigonometry possesses not only abstract beauty but offers concrete solutions for complex construction tasks, showing how mathematical elegance elegantly solves practical problems.