Hyperboloid Calculator
Calculator and formulas for calculating a hyperboloid
Hyperboloid Calculator
The Hyperboloid
The hyperboloid is a hyperbolic surface of revolution with a characteristic waist shape.
Hyperboloid Properties
The Hyperboloid: Surface of revolution of a hyperbola around its axis of symmetry
Hyperboloid Visualization
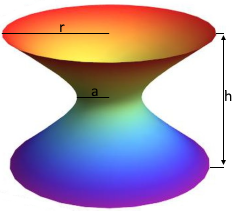
Hyperboloid
Surface of revolution with characteristic waist shape
Parameters
r: Base radius (largest radius)
a: Center radius (waist)
h: Total height
Image by Anton Sel, CC BY-SA 4.0, via Wikimedia Commons
Hyperbolic surface of revolution.
Mathematical elegance in 3D.
|
|
What is a Hyperboloid?
The hyperboloid is a fascinating geometric body:
- Definition: Surface of revolution of a hyperbola around its axis of symmetry
- Shape: Characteristic waist shape with narrowest point in the center
- Parameters: Base radius r, center radius a, and height h
- Type: One-sheet hyperboloid (hyperboloid of one sheet)
- Applications: Architecture, engineering, cooling tower construction
- Mathematics: Quadratic equation in three variables
Geometric Properties of the Hyperboloid
The hyperboloid shows remarkable geometric properties:
Basic Parameters
- Base radius r: Largest radius at the ends
- Center radius a: Smallest radius at the waist
- Height h: Total height of the hyperboloid
- Shape parameter c: Determines the curvature of the hyperbola
Special Properties
- Rotational symmetry: Symmetry around the vertical axis
- Hyperbolic meridians: Each meridional section is a hyperbola
- Circular cross-sections: All horizontal sections are circles
- Ruled surface property: Can be generated by straight lines
Mathematical Relationships of the Hyperboloid
The hyperboloid follows elegant mathematical laws:
Volume Formula
The volume elegantly combines both radii. Mathematical beauty.
Shape Parameter c
The shape parameter determines the curvature of the hyperbolic form.
Applications of the Hyperboloid
Hyperboloids find applications in various fields:
Architecture & Construction
- Cooling tower constructions
- Modern skyscrapers and towers
- Bridge elements and structures
- Shell structures and domes
Engineering
- Steam turbines and rotors
- Aerodynamic components
- Pressure vessels and reactors
- Flow-guiding components
Science & Research
- Particle accelerators
- Optical systems
- Astronomical instruments
- Materials science
Art & Design
- Sculptural works
- Architectural highlights
- Industrial design
- Mathematical art
Formulas for the Hyperboloid
Volume (V)
Volume of the one-sheet hyperboloid
Shape Parameter (c)
Parameter describing the hyperbolic curvature
Base Radius from a and c
Reverse calculation of the base radius
Hyperbolic Equation
Standard form of the one-sheet hyperboloid
Hyperboloid Properties
One-sheet hyperboloid
Hyperbolic
Rotationally symmetric
Circular
The hyperboloid combines hyperbolic curvature with rotationally symmetric elegance
Calculation Example for a Hyperboloid
Given
Find: Volume and shape parameter of the hyperboloid
1. Volume Calculation
For r = 8 cm, a = 4 cm, h = 10 cm:
\[V = \frac{1}{3} \cdot \pi \cdot h \cdot (2a^2 + r^2)\] \[V = \frac{1}{3} \cdot \pi \cdot 10 \cdot (2 \cdot 16 + 64)\] \[V = \frac{1}{3} \cdot \pi \cdot 10 \cdot (32 + 64)\] \[V = \frac{1}{3} \cdot \pi \cdot 10 \cdot 96 = 320\pi ≈ 1005.31 \text{ cm}^3\]The volume is approximately 1005.31 cm³
2. Shape Parameter Calculation
Calculation of parameter c:
\[\frac{r^2}{a^2} = \frac{64}{16} = 4\] \[\frac{r^2}{a^2} - 1 = 4 - 1 = 3\] \[c = \sqrt{\frac{h^2}{4 \cdot 3}} = \sqrt{\frac{100}{12}} = \sqrt{8.333}\] \[c ≈ 2.89 \text{ cm}\]The shape parameter c is approximately 2.89 cm
3. Geometric Analysis
Geometric characteristics:
Waist ratio:\[\frac{a}{r} = \frac{4}{8} = 0.5\] Height-radius ratio:
\[\frac{h}{r} = \frac{10}{8} = 1.25\] Curvature parameter:
\[\frac{c}{a} = \frac{2.89}{4} ≈ 0.72\]
The hyperboloid has a pronounced waist shape
4. Verification Calculation
Reverse calculation of base radius:
\[r = a \cdot \sqrt{1 + \frac{h^2}{4c^2}}\] \[r = 4 \cdot \sqrt{1 + \frac{100}{4 \cdot 8.333}}\] \[r = 4 \cdot \sqrt{1 + 3} = 4 \cdot 2 = 8 \text{ cm}\]The verification confirms r = 8 cm
5. Summary
The hyperboloid with characteristic waist shape and all parameters
6. Practical Example: Cooling Tower
V ≈ 1005.31 cm³
≈ 1.01 liters
Waist: 50% of base radius
Material savings
Hyperbolic shape
Optimal airflow
A cooling tower with hyperbolic shape optimizes flow and material consumption
7. Comparison with Cylinder
r=8, a=4, h=10
V≈1005.31 cm³
r=8, h=10
V≈2010.62 cm³
≈ 50% of cylinder volume
More efficient!
The hyperboloid has about half the volume of a corresponding cylinder
The Hyperboloid: Mathematical Elegance in Architecture
The hyperboloid is one of the most fascinating geometric shapes that unites mathematical elegance with practical functionality. As a surface of revolution of a hyperbola around its axis of symmetry, it creates a characteristic waist shape that is not only aesthetically pleasing but also offers structural and flow-dynamic advantages. This unique combination of mathematical precision and practical utility makes the hyperboloid a preferred element in modern architecture and engineering.
The Geometry of the Hyperbola
The hyperboloid shows the perfection of hyperbolic geometry:
- Hyperbolic meridians: Each vertical section shows a hyperbola
- Circular cross-sections: All horizontal sections are perfect circles
- Waist shape: Narrowest point in the center at radius a
- Rotational symmetry: Infinite symmetry planes through the axis
- Ruled surface property: Can be generated by straight lines
- Parametric description: Elegant mathematical formulas
- Quadratic equation: x²/a² + y²/a² - z²/c² = 1
Architectural Masterpieces
Cooling Tower Revolution
Hyperbolic cooling towers optimize airflow and material consumption through their characteristic waist shape and create iconic silhouettes.
Structural Superiority
The hyperbolic shape offers optimal load distribution and stability with minimal material usage in skyscrapers and towers.
Flow Optimization
In engineering, hyperbolic profiles enable optimal flow guidance in turbines, nozzles, and aerodynamic components.
Aesthetic Innovation
As a sculptural element, the hyperboloid embodies the perfect synthesis of mathematical precision and artistic expression.
Summary
The hyperboloid embodies the perfect harmony between mathematical elegance and practical functionality. Its waist shape, created by hyperbolic rotation and described by the elegant volume formula V = (π/3)h(2a²+r²), makes it one of the most versatile and efficient geometric bodies. The combination of structural stability, material savings, and flow-optimal properties shows how mathematical precision creates practical advantages. From the iconic cooling towers of power plants to modern skyscrapers to precise turbine blades - the hyperboloid proves that the most beautiful geometric shapes are often also the most functional. It is living proof that mathematics not only possesses abstract beauty but also provides concrete solutions for complex technical challenges while creating aesthetic masterpieces that shape our built environment.