Truncated Cylinder Calculator
Calculator and formulas for calculating an oblique cylinder section
Truncated Cylinder Calculator
The Truncated Cylinder
The truncated cylinder is a diagonally cut cylinder with different heights.
Truncated Cylinder Properties
The Truncated Cylinder: Diagonally cut cylinder with elliptical cut surfaces
Truncated Cylinder Visualization
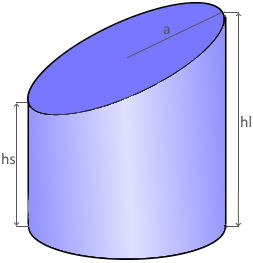
Truncated Cylinder
Diagonally cut cylinder
Parameters
r: Radius of the base
hs: Short height (minimum)
hl: Long height (maximum)
a: Major semi-axis of the ellipse
Diagonally cut cylinder.
Elliptical cut surfaces.
|
|
What is a Truncated Cylinder?
The truncated cylinder is a fascinating geometric body:
- Definition: Cylinder part created by an oblique cut
- Characteristics: Two different heights hs and hl
- Properties: Elliptical top and bottom surfaces
- Cut angle: Determines the elliptical shape of the cut surfaces
- Applications: Piping, architecture, mechanical engineering
- Mathematics: Combination of cylinder and ellipse geometry
Geometric Properties of the Truncated Cylinder
The truncated cylinder shows characteristic geometric properties:
Basic Parameters
- Radius r: Radius of the circular base
- Short height hs: Minimum height of the section
- Long height hl: Maximum height of the section
- Average height: hm = (hs + hl)/2
Special Properties
- Elliptical cut surfaces: Created by oblique cutting
- Trapezoidal lateral surface: Side surface can be unfolded as trapezoid
- Ellipse semi-axis: a = √(r² + ((hl-hs)/2)²)
- Volume conservation: Average height determines the volume
Mathematical Relationships of the Truncated Cylinder
The truncated cylinder follows elegant mathematical laws:
Volume Formula
The volume is determined by the average height. Elegant averaging principle.
Ellipse Semi-axis
The major semi-axis of the elliptical cut surfaces by Pythagoras theorem.
Applications of the Truncated Cylinder
Truncated cylinders find applications in various fields:
Piping Technology
- Oblique pipe connections
- Transition pieces between pipelines
- Pipe branches
- Flange connections
Architecture & Construction
- Roof constructions
- Oblique column connections
- Stair railings
- Architectural details
Mechanical Engineering & Automotive
- Gear shafts
- Coupling elements
- Exhaust systems
- Hydraulic components
Process Engineering
- Oblique container openings
- Funnel elements
- Dosing devices
- Conveyor systems
Formulas for the Truncated Cylinder
Volume (V)
Volume through average height
Base Area (A)
Circular base area
Lateral Area (L)
Trapezoidal lateral surface
Semi-axis (a)
Major semi-axis of the ellipse
Total Surface Area (S)
Lateral area plus elliptical top and bottom surfaces
Additional Parameters
\[P = 2\pi r\]
\[h_m = \frac{h_s + h_l}{2}\]
\[\Delta h = h_l - h_s\]
\[\tan \alpha = \frac{\Delta h}{2r}\]
The truncated cylinder combines cylinder and ellipse geometry
Calculation Example for a Truncated Cylinder
Given
Find: All parameters of the truncated cylinder
1. Average Height and Volume
For r = 5 cm, hs = 4 cm, hl = 6 cm:
\[h_m = \frac{h_s + h_l}{2} = \frac{4 + 6}{2} = 5 \text{ cm}\] \[V = \pi r^2 h_m = \pi \cdot 25 \cdot 5 = 125\pi\] \[V ≈ 392.70 \text{ cm}^3\]The volume is approximately 392.70 cm³
2. Ellipse Semi-axis
Major semi-axis of the cut ellipse:
\[\frac{h_l - h_s}{2} = \frac{6 - 4}{2} = 1 \text{ cm}\] \[a = \sqrt{r^2 + 1^2} = \sqrt{25 + 1}\] \[a = \sqrt{26} ≈ 5.10 \text{ cm}\]The ellipse semi-axis is approximately 5.10 cm
3. Base Area Calculation
Base area and perimeter:
\[A = \pi r^2 = \pi \cdot 25 ≈ 78.54 \text{ cm}^2\] \[P = 2\pi r = 10\pi ≈ 31.42 \text{ cm}\]Base area ≈ 78.54 cm², Perimeter ≈ 31.42 cm
4. Lateral Area Calculation
Trapezoidal lateral surface:
\[L = \pi r (h_s + h_l)\] \[L = \pi \cdot 5 \cdot (4 + 6)\] \[L = 50\pi ≈ 157.08 \text{ cm}^2\]The lateral area is approximately 157.08 cm²
5. Total Surface Area
Complete surface area calculation:
\[S = L + \pi r (r + a)\] \[S = 157.08 + \pi \cdot 5 \cdot (5 + 5.10)\] \[S = 157.08 + 15.7\pi \cdot 10.10\] \[S ≈ 157.08 + 497.87 ≈ 654.95 \text{ cm}^2\]The total surface area is approximately 654.95 cm²
6. Geometric Analysis
tan(α) = Δh/(2r) = 2/10 = 0.2
α ≈ 11.31°
a/r = 5.10/5 ≈ 1.02
Slightly elliptical
hl/hs = 6/4 = 1.5
50% height difference
The truncated cylinder shows moderate oblique cutting
7. Summary
The truncated cylinder with all characteristic parameters
8. Practical Example: Pipe Branch
V ≈ 392.70 cm³
≈ 0.39 liters
S ≈ 654.95 cm²
Sheet consumption
Gentle transition
α = 11.31° inclination
A pipe branch with optimal flow guidance and minimal pressure loss
9. Comparison with Regular Cylinder
r=5, hs=4, hl=6
V≈392.70 cm³
r=5, h=5
V≈392.70 cm³
Same volume!
Average height decides
The volume is determined only by the average height - elegant geometry!
The Truncated Cylinder: Elegance of Cut Geometry
The truncated cylinder is a fascinating geometric body that combines the elegance of classical cylinder geometry with the complexity of elliptical cut surfaces. As a cylinder part created by an oblique cut, it unites the practicality of cylindrical forms with the mathematical sophistication of elliptical geometry. This unique combination makes it an indispensable element in piping technology, architecture, and mechanical engineering, where precise transitions and optimal flow guidance are crucial.
The Geometry of the Oblique Cut
The truncated cylinder shows the perfection of controlled cut geometry:
- Two characteristic heights: hs (short) and hl (long) define the form
- Average height hm = (hs+hl)/2: Elegantly determines the volume
- Elliptical cut surfaces: Ellipses created by oblique cutting
- Trapezoidal lateral surface: Unfoldable to a perfect trapezoid
- Semi-axis relationship: a = √(r² + ((hl-hs)/2)²) by Pythagoras
- Inclination angle α: tan(α) = (hl-hs)/(2r) for flow optimization
- Volume conservation: Only the average height determines the volume
Versatile Applications
Piping Technology
Oblique pipe sections enable smooth transitions between different pipeline levels and optimize flow behavior with minimal pressure losses.
Architectural Elegance
In architecture, truncated cylinders create flowing transitions between different building areas and enable innovative roof constructions.
Mechanical Engineering Precision
Precisely manufactured truncated cylinders in gears and couplings ensure optimal power transmission with compact construction.
Process Engineering Efficiency
Oblique container openings and funnel elements utilize gravity optimally and significantly improve emptying and dosing.
Summary
The truncated cylinder embodies the perfect synthesis of geometric precision and practical functionality. Its form, characterized by oblique cutting and described by the elegant volume formula V = πr²(hs+hl)/2, shows how the average height determines the entire volume - a triumph of mathematical elegance. The elliptical cut surfaces with their semi-axis relationship a = √(r² + ((hl-hs)/2)²) demonstrate the perfect application of the Pythagorean theorem in practical geometry. From optimized pipe connections to elegant architectural elements to precise mechanical components - the truncated cylinder proves that the most beautiful geometric solutions often arise from the combination of simple principles. It is living proof that controlled asymmetry leads to perfect functionality and shows how cut geometry elegantly and efficiently solves practical problems.